AT_abc358_f [ABC358F] Easiest Maze
题目描述
すぬけ君打算在 AtCoder Land 建造一个新的迷宫作为亮点项目。迷宫可以表示为一个纵向 $N$ 行、横向 $M$ 列的网格,右上角格子的上边是入口,右下角格子的下边是出口。すぬけ君可以通过在相邻格子之间适当设置墙壁来构建迷宫。
すぬけ君非常喜欢简单的迷宫,因此他希望从入口到出口的路径没有任何分支,并且恰好经过 $K$ 个格子。请判断是否可以构建这样的迷宫,如果可以,请构建出其中一种方案。
例如,下图中 $N=3, M=3$,实线表示墙壁的位置(除入口和出口外,外周必定有墙壁)。此时,从入口到出口的路径没有任何分支,且恰好经过了 $7$ 个格子。
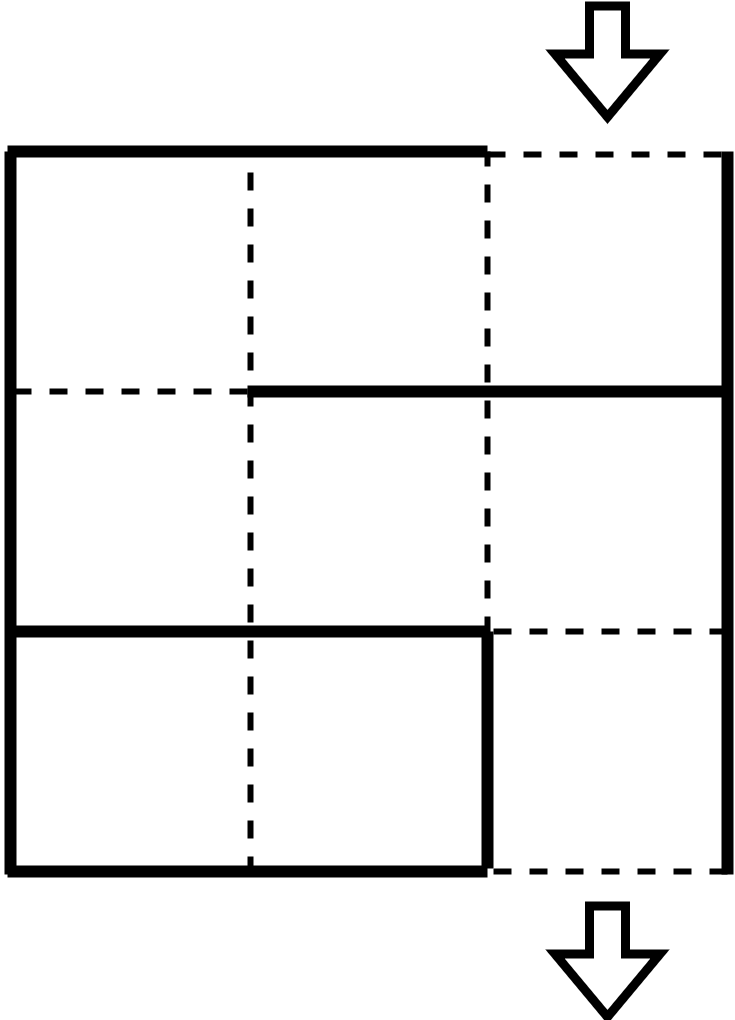
具体要求如下:
有一个纵向 $N$ 行、横向 $M$ 列的网格。第 $i$ 行第 $j$ 列的格子记为 $(i,j)$。你可以决定是否在每对相邻格子之间放置墙壁。请判断是否可以通过合理设置墙壁,使得满足以下条件,并在可能的情况下给出一种构造方案。
> 考虑一个有 $NM$ 个顶点的无向图 $G$。$G$ 的每个顶点用一对整数 $(i,j)\ (1\leq i\leq N,\ 1\leq j\leq M)$ 唯一标记。对于两个不同的顶点 $(i_1,j_1),(i_2,j_2)$,如果 $|i_1-i_2|+|j_1-j_2|=1$ 且这两个格子之间没有墙壁,则它们之间有一条边。
>
> 条件:存在一条包含 $K$ 个顶点、连接 $(1,M)$ 和 $(N,M)$ 的简单路径,并且包含 $(1,M)$ 和 $(N,M)$ 的连通分量仅由这条路径组成。
输入格式
输入通过标准输入给出,格式如下:
> $N$ $M$ $K$
输出格式
如果不存在满足条件的墙壁配置,则输出 `No`。如果存在,则输出其中一种方案,格式如下。若有多种满足条件的墙壁配置,输出任意一种均可。
**由于输出格式较为复杂,请参考下方的输出示例。**
> Yes
> +++++...+++S+
> +o?o?...?o?o+
> +?+?+...+?+?+
> +o?o?...?o?o+
> +?+?+...+?+?+
> ⋮
> +o?o?...?o?o+
> +?+?+...+?+?+
> +o?o?...?o?o+
> +++++...+++G+
其中,`S`、`G`、`+`、`o` 分别表示入口、出口、墙壁、格子。格子与格子之间的 `?` 表示可以放置墙壁的位置。对于横向相邻的两个格子之间的 `?`,若放置墙壁则用 `|`,不放则用 `.`。对于纵向相邻的两个格子之间的 `?`,若放置墙壁则用 `-`,不放则用 `.`。
具体说明如下:
- 输出共 $2N+2$ 行,第 $1$ 行输出字符串 `Yes`,第 $2$ 行到第 $2N+2$ 行按如下方式输出,每行长度为 $2M+1$。
- 第 $2$ 行输出 $2M-1$ 个 `+`,`S`,`+`,依次连接。
- 第 $1+2i$ 行($1\leq i\leq N$):`+`,`o`,$c_{i,1}$,`o`,$c_{i,2}$,$\dots$,$c_{i,M-1}$,`o`,`+`,依次连接。$c_{i,j}$ 表示 $(i,j)$ 和 $(i,j+1)$ 之间,若放墙壁则为 `|`,否则为 `.`。
- 第 $2+2i$ 行($1\leq i\leq N-1$):`+`,$r_{i,1}$,`+`,$r_{i,2}$,`+`,$\dots$,`+`,$r_{i,M}$,`+`,依次连接。$r_{i,j}$ 表示 $(i,j)$ 和 $(i+1,j)$ 之间,若放墙壁则为 `-`,否则为 `.`。
- 第 $2N+2$ 行输出 $2M-1$ 个 `+`,`G`,`+`,依次连接。
说明/提示
### 数据范围
- $2\leq N \leq 100$
- $1\leq M \leq 100$
- $1\leq K\leq NM$
- 输入均为整数
### 样例解释 1
与题目描述中的图示墙壁配置相同。
由 ChatGPT 4.1 翻译