AT_abc376_b [ABC376B] Hands on Ring (Easy)

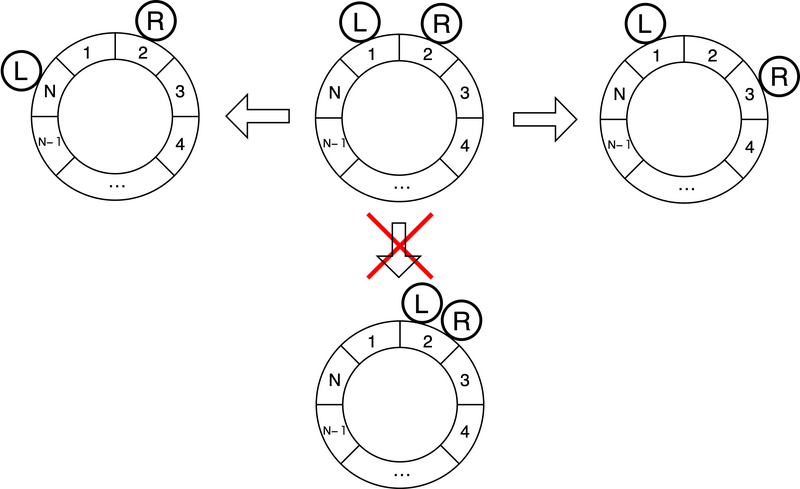
[problemUrl]: https://atcoder.jp/contests/abc376/tasks/abc376_b **注意：本题与 F 问题的设定几乎相同，仅有正文中加粗部分及约束条件不同。** 你正用双手握住一个环。这个环由 $N\ (N\geq 3)$ 个部件 $1,2,\dots,N$ 组成，部件 $i$ 与部件 $i+1$（$1\leq i\leq N-1$），以及部件 $1$ 与部件 $N$ 彼此相邻。 最初，左手握住部件 $1$，右手握住部件 $2$。你可以在一次*操作*中做如下事情： - 将一只手移动到当前握住的部件相邻的任意一个部件上，但前提是目标部件上没有另一只手。 下图展示了初始状态，以及从该状态出发可以进行和不能进行的操作示例。环上每个部件上的数字表示该部件的编号，标有 L 的圆圈表示左手，标有 R 的圆圈表示右手。  接下来你需要依次按照给定的 $Q$ 个指令操作。第 $i\ (1\leq i\leq Q)$ 个指令由字符 $H_i$ 和整数 $T_i$ 表示，其含义如下： - 通过若干次操作（可以为 $0$ 次），使得如果 $H_i$ 为 `L`，则左手握住部件 $T_i$；如果 $H_i$ 为 `R`，则右手握住部件 $T_i$。此时，**不允许移动 $H_i$ 指定的手以外的另一只手**。 **保证所有给定的指令都是可达的。** 在本题设定下，可以证明对于每个 $i$，在执行第 $i$ 个指令前，两只手的位置是唯一确定的。此时，设左手位置为 $l_i$，右手位置为 $r_i$，则若 $H_i=$ `L`，有 $T_i\neq r_i$；若 $H_i=$ `R`，有 $T_i\neq l_i$。 请你求出，为了依次完成所有指令，所需操作次数的最小总和。

输入按以下格式从标准输入读入。 > $N$ $Q$ $H_1$ $T_1$ $H_2$ $T_2$ $\vdots$ $H_Q$ $T_Q$

请输出依次完成所有指令所需操作次数的最小总和。

### 约束条件 - $3\leq N \leq 100$ - $1\leq Q \leq 100$ - $H_i$ 为 `L` 或 `R` - $1\leq T_i\leq N$ - $N,Q,T_i$ 均为整数 - 所有指令均可达（详见题目描述） ### 样例解释 1  可以按如下方式依次完成 $Q$ 个指令： 1. 右手依次移动到部件 $2\rightarrow 3\rightarrow 4$，完成第 $1$ 个指令。 2. 左手依次移动到部件 $1\rightarrow 6\rightarrow 5$，完成第 $2$ 个指令。 3. 右手依次移动到部件 $4\rightarrow 3\rightarrow 2\rightarrow 1\rightarrow 6$，完成第 $3$ 个指令。 此时总操作次数为 $2+2+4=8$，且这是最小值。（注意，完成第 $3$ 个指令时，右手不能走 $4\rightarrow 5\rightarrow 6$ 这条路径。） ### 样例解释 2 有时可以在不进行任何操作的情况下完成所有指令。 由 ChatGPT 4.1 翻译