AT_abc376_b [ABC376B] Hands on Ring (Easy)

[problemUrl]: https://atcoder.jp/contests/abc376/tasks/abc376_b **注：この問題は F 問題とほぼ同じ設定です。本文中で太字で示されている部分および制約のみが異なります。** あなたはあるリングを両手で握っています。 このリングは $ N\ (N\geq\ 3) $ 個のパーツ $ 1,2,\dots,N $ によって構成されており、パーツ $ i $ とパーツ $ i+1 $ ($ 1\leq\ i\leq\ N-1 $)、およびパーツ $ 1 $ とパーツ $ N $ がそれぞれ隣接しています。 最初、左手はパーツ $ 1 $ を、右手はパーツ $ 2 $ を握っています。 あなたは、$ 1 $ 回の *操作* で以下のことを行えます。 - 片方の手を、今握っているパーツに隣接するいずれかのパーツに移動する。ただし、移動先にもう一方の手がない場合に限る。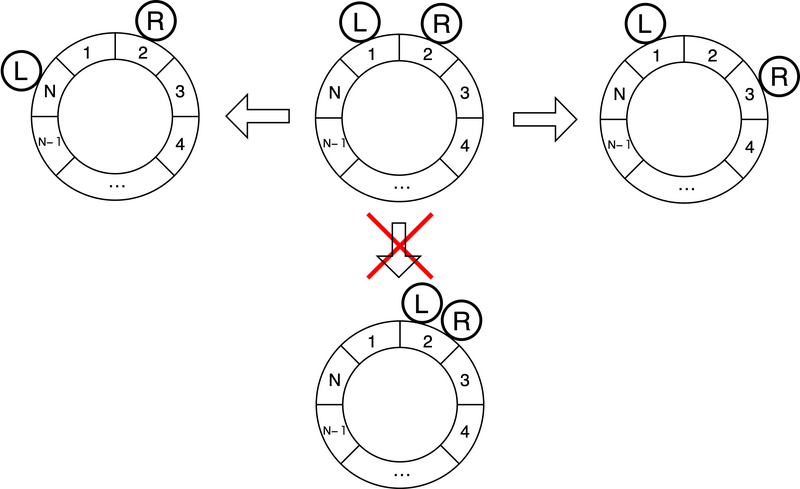 以下の図は、初期状態およびそこから行える操作と行えない操作の例を示したもので、リングの各パーツに書き込まれた数はそのパーツの番号を、L と書かれた丸は左手を、R と書かれた丸は右手を示しています。  あなたは今から与えられる $ Q $ 個の指示に順番に従う必要があります。 $ i\ (1\leq\ i\leq\ Q) $ 個目の指示は文字 $ H_i $ および整数 $ T_i $ によって表され、その意味は以下の通りです： - 操作を何回か（$ 0 $ 回でもよい）行うことで、$ H_i $ が `L` ならば左手、`R` ならば右手が、パーツ $ T_i $ を握っている状態にする。 このとき、$ H_i $ によって指定された手ではない方の手を **動かしてはならない**。 **なお、達成可能な指示しか与えられないことが保証されます。** 詳細この問題の設定の下では、各 $ i $ について、$ i $ 個目の指示に従う直前でのそれぞれの手の位置が一意に定まることが証明できます。 このとき、左手の位置をパーツ $ l_i $、右手の位置をパーツ $ r_i $ とおくと、$ H_i= $ `L` ならば $ T_i\neq\ r_i $ が、$ H_i= $ `R` ならば $ T_i\neq\ l_i $ がそれぞれ保証されます。 すべての指示に従うために必要な操作回数の合計の最小値を求めてください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ Q $ $ H_1 $ $ T_1 $ $ H_2 $ $ T_2 $ $ \vdots $ $ H_Q $ $ T_Q $

すべての指示に従うために必要な操作回数の合計の最小値を出力せよ。

### 制約 - $ 3\leq\ N\ \leq\ 100 $ - $ 1\leq\ Q\ \leq\ 100 $ - $ H_i $ は `L` または `R` - $ 1\leq\ T_i\leq\ N $ - $ N,Q,T_i $ は整数 - 達成可能な指示しか与えられない（詳細は問題文を参照してください） ### Sample Explanation 1  以下のように操作を行うことで、$ Q $ 個の指示すべてに順番に従うことができます。 1. 右手をパーツ $ 2\rightarrow\ 3\rightarrow\ 4 $ と移動させることで、$ 1 $ 番目の指示に従う。 2. 左手をパーツ $ 1\rightarrow\ 6\rightarrow\ 5 $ と移動させることで、$ 2 $ 番目の指示に従う。 3. 右手をパーツ $ 4\rightarrow\ 3\rightarrow\ 2\rightarrow\ 1\rightarrow\ 6 $ と移動させることで、$ 3 $ 番目の指示に従う。 このとき行う操作回数の合計は $ 2+2+4=8 $ であり、これが最小です。 （$ 3 $ 番目の指示に従う際に右手をパーツ $ 4\rightarrow\ 5\rightarrow\ 6 $ と移動させることはできないことに注意してください。） ### Sample Explanation 2 操作を $ 1 $ 度も行わずに指示に従うことができる場合もあります。