AT_abc377_b [ABC377B] Avoid Rook Attack

有一个由 $8$ 行 $8$ 列共 $64$ 个格子组成的棋盘。我们将从上往下的第 $i$ 行（$1\leq i\leq 8$）、从左往右的第 $j$ 列（$1\leq j\leq 8$）的格子称为格子 $(i,j)$。 每个格子要么是空格，要么已经有棋子放置。棋盘的状态由一个长度为 $8$ 的字符串序列 $(S_1, S_2, S_3, \ldots, S_8)$ 表示。对于格子 $(i,j)$（$1\leq i\leq 8, 1\leq j\leq 8$），如果 $S_i$ 的第 $j$ 个字符为 `.`，则该格子为空；如果为 `#`，则该格子上有一个棋子。 你想在任意一个**空格**上放置你自己的棋子，并且要保证**不会被已经放置的任何棋子吃掉**。 对于放在 $(i,j)$ 的棋子，如果满足以下任一条件，则可以吃掉其他棋子： - 在第 $i$ 行的格子上放置的棋子 - 在第 $j$ 列的格子上放置的棋子 例如，放在 $(4,4)$ 的棋子可以吃掉下图中蓝色标记的格子上的棋子。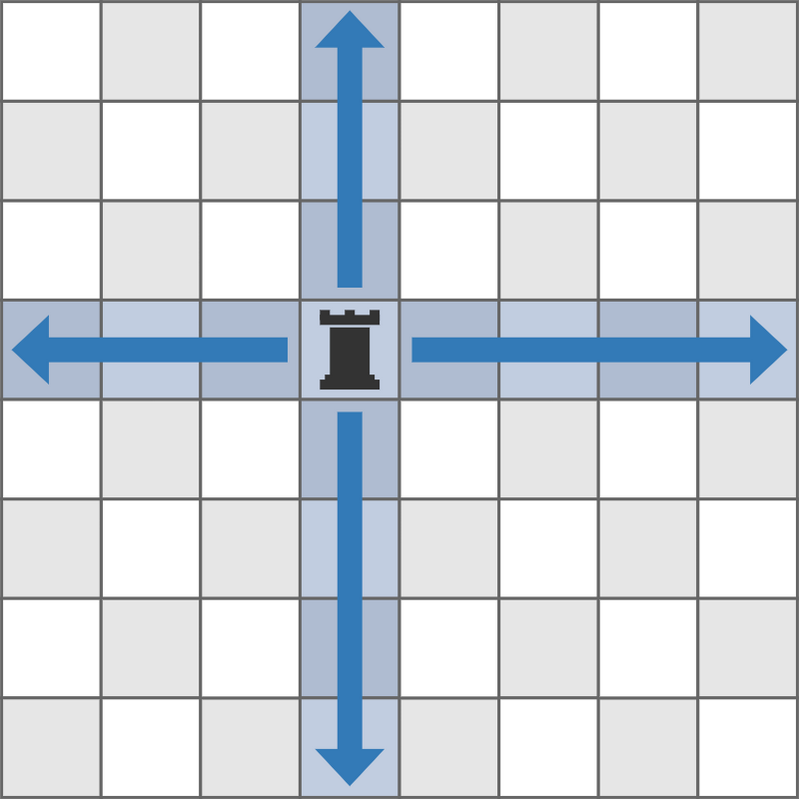  请你计算，有多少个格子可以放置你的棋子，并且不会被已经放置的任何棋子吃掉。

输入从标准输入中给出，格式如下： > $S_1$ > $S_2$ > $S_3$ > $S_4$ > $S_5$ > $S_6$ > $S_7$ > $S_8$

输出一个整数，表示可以放置你的棋子且不会被已有棋子吃掉的空格数量。

### 限制条件 - $S_i$ 是由 `.` 和 `#` 组成的长度为 $8$ 的字符串（$1\leq i\leq 8$） ### 样例解释 1 已经放置的棋子可以吃掉下图中蓝色标记的格子上的棋子。  因此，你可以安全放置棋子的格子为 $(6,6)$、$(6,7)$、$(7,6)$、$(7,7)$ 共 $4$ 个格子。 ### 样例解释 2 也有可能没有任何棋子被放置。 由 ChatGPT 4.1 翻译