AT_abc377_c [ABC377C] Avoid Knight Attack

[problemUrl]: https://atcoder.jp/contests/abc377/tasks/abc377_c 縦 $ N $ マス、横 $ N $ マスの $ N\ ^\ 2 $ マスからなるマス目があります。 上から $ i $ 行目 $ (1\leq\ i\leq\ N) $ 、左から $ j $ 列目 $ (1\leq\ j\leq\ N) $ のマスをマス $ (i,j) $ と呼ぶことにします。 それぞれのマスは、空マスであるかコマが置かれているかのどちらかです。 マス目には合計で $ M $ 個のコマが置かれており、$ k $ 番目 $ (1\leq\ k\leq\ M) $ のコマはマス $ (a\ _\ k,b\ _\ k) $ に置かれています。 あなたは、すでに置かれている**どのコマにも取られないように**、いずれかの**空マス**に自分のコマを置きたいです。 マス $ (i,j) $ に置かれているコマは、次のどれかの条件を満たすコマを取ることができます。 - マス $ (i+2,j+1) $ に置かれている - マス $ (i+1,j+2) $ に置かれている - マス $ (i-1,j+2) $ に置かれている - マス $ (i-2,j+1) $ に置かれている - マス $ (i-2,j-1) $ に置かれている - マス $ (i-1,j-2) $ に置かれている - マス $ (i+1,j-2) $ に置かれている - マス $ (i+2,j-1) $ に置かれている ただし、存在しないマスについての条件は常に満たされないものとします。 たとえば、マス $ (4,4) $ に置かれているコマは、以下の図で青く示されたマスに置かれているコマを取ることができます。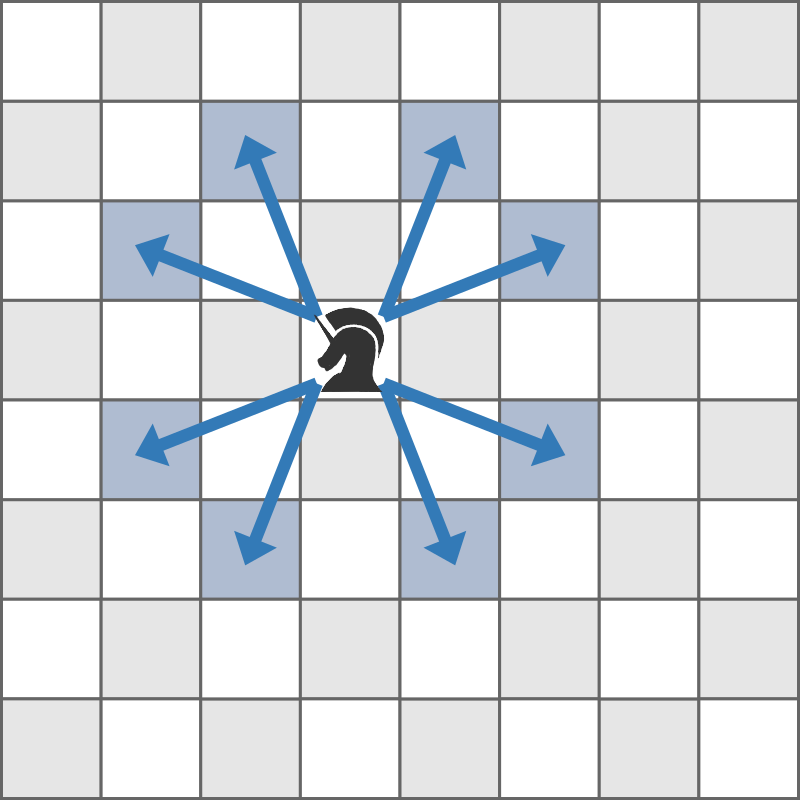  あなたがコマを置くことができるマスがいくつあるか求めてください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ a\ _\ 1 $ $ b\ _\ 1 $ $ a\ _\ 2 $ $ b\ _\ 2 $ $ \vdots $ $ a\ _\ M $ $ b\ _\ M $

すでに置かれているコマに取られずに自分のコマを置くことができる空マスの個数を出力せよ。

### 制約 - $ 1\leq\ N\leq10\ ^\ 9 $ - $ 1\leq\ M\leq2\times10\ ^\ 5 $ - $ 1\leq\ a\ _\ k\leq\ N,1\leq\ b\ _\ k\leq\ N\ (1\leq\ k\leq\ M) $ - $ (a\ _\ k,b\ _\ k)\neq(a\ _\ l,b\ _\ l)\ (1\leq\ k\lt\ l\leq\ M) $ - 入力はすべて整数 ### Sample Explanation 1 すでに置かれているコマは、以下の図で青く示されたマスに置かれたコマを取ることができます。  よって、あなたがすでに置かれているコマに取られないように自分のコマを置くことができるマスは残りの $ 38 $ マスです。 ### Sample Explanation 2 $ 10\ ^\ {18} $ マスのうち、置くことができないマスはマス $ (1,1),(2,3),(3,2) $ の $ 3 $ マスのみです。 答えが $ 2\ ^\ {32} $ 以上になる場合があることに注意してください。