AT_abc382_f [ABC382F] Falling Bars

有一个 $H$ 行 $W$ 列的网格。我们用 $(i,j)$ 表示从上往下第 $i$ 行、从左往右第 $j$ 列的格子（$1\leq i\leq H$，$1\leq j\leq W$）。 在这个网格上放置了 $N$ 个编号为 $1$ 到 $N$ 的横向长条。第 $i$ 个长条由 $L_i$ 个 $1\times 1$ 的方块横向相连组成，其最左端的方块最初位于格子 $(R_i,C_i)$。也就是说，第 $i$ 个长条最初占据 $(R_i,C_i),\ (R_i,C_i+1),\ \dots,\ (R_i,C_i+L_i-1)$ 这些格子。保证不存在被两个不同长条同时占据的格子。 当前时刻为 $t=0$。对于所有可以表示为 $t=0.5+n$ 的时刻（$n$ 为非负整数），依次对 $i=1,2,\dots,N$ 执行以下操作： - 如果第 $i$ 个长条没有在最底下的一行（即第 $H$ 行），并且它所占据的每个格子的正下方格子都没有被任何长条占据，则第 $i$ 个长条整体向下移动一格。也就是说，如果此时第 $i$ 个长条占据 $(r,C_i),(r,C_i+1),\dots,(r,C_i+L_i-1)$（$r

输入按以下格式从标准输入给出。 > $H$ $W$ $N$ > $R_1$ $C_1$ $L_1$ > $R_2$ $C_2$ $L_2$ > $\vdots$ > $R_N$ $C_N$ $L_N$

输出 $N$ 行。第 $i$ 行输出 $R'_i$。

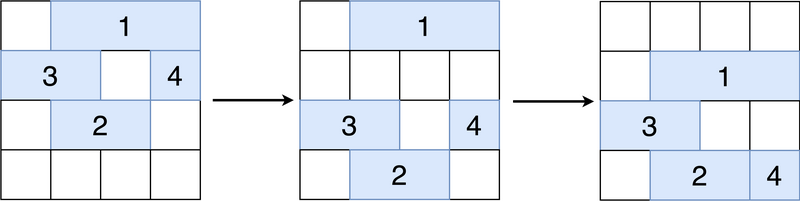
## 限制条件 - $1\leq H,W \leq 2\times 10^5$ - $1\leq N \leq 2\times 10^5$ - $1\leq R_i\leq H$ - $1\leq C_i\leq W$ - $1\leq L_i\leq W-C_i+1$ - 在给定的初始状态下，不存在被两个不同长条同时占据的格子 - 输入均为整数 ## 样例解释 1 下图从左到右分别表示 $t=0,1,2$ 时的网格状态。带颜色的长方形表示各个长条，长方形内的数字为该长条的编号。  网格状态的变化如下所述： - $t=0.5$： - $i=1$：第 1 个长条下方的 $(2,2),(2,3),(2,4)$ 中，$(2,2)$ 被第 3 个长条占据，$(2,4)$ 被第 4 个长条占据，因此不移动。 - $i=2$：第 2 个长条下方的 $(4,2),(4,3)$ 都没有被其他长条占据，因此整体下移一格。 - $i=3$：第 3 个长条下方的 $(3,1),(3,2)$ 都没有被其他长条占据，因此整体下移一格。 - $i=4$：第 4 个长条下方的 $(3,4)$ 没有被其他长条占据，因此整体下移一格。 - $t=1.5$： - $i=1$：第 1 个长条下方的 $(2,2),(2,3),(2,4)$ 都没有被其他长条占据，因此整体下移一格。 - $i=2$：第 2 个长条已在最底下一行，不移动。 - $i=3$：第 3 个长条下方的 $(4,1),(4,2)$ 中，$(4,2)$ 被第 2 个长条占据，因此不移动。 - $i=4$：第 4 个长条下方的 $(4,4)$ 没有被其他长条占据，因此整体下移一格。 - $t=2.5,3.5,\dots$ 时，没有任何长条能整体下移，因此 $t=10^{100}$ 时网格状态与 $t=2$ 时相同（即上图最右侧状态）。 因此，$R'_1=2,R'_2=4,R'_3=3,R'_4=4$。 由 ChatGPT 4.1 翻译