AT_abc382_g [ABC382G] Tile Distance 3
题目描述
在二维坐标平面上铺满了瓷砖。
每块瓷砖的形状都是长方形,对于满足 $0 \leq k < K$ 的每组整数 $(i, j, k)$,按照以下规则放置对应的瓷砖。
- 当 $i$ 与 $j$ 的奇偶性相同时,与 $(i, j, k)$ 对应的瓷砖覆盖满足 $iK \leq x \leq (i+1)K$ 且 $jK + k \leq y \leq jK + k + 1$ 的所有 $(x, y)$。
- 当 $i$ 与 $j$ 的奇偶性不同时,与 $(i, j, k)$ 对应的瓷砖覆盖满足 $iK + k \leq x \leq iK + k + 1$ 且 $jK \leq y \leq (j+1)K$ 的所有 $(x, y)$。
定义两块瓷砖**相邻**,当且仅当它们的边有正长度的公共部分。
从包含点 $(S_x + 0.5, S_y + 0.5)$ 的瓷砖出发,每次可以移动到相邻的瓷砖,求到达包含点 $(T_x + 0.5, T_y + 0.5)$ 的瓷砖所需移动到相邻瓷砖的最小次数。
给定 $T$ 组测试数据,请分别输出每组的答案。
输入格式
输入以以下格式从标准输入给出。
> $T$
> $\text{case}_1$
> $\vdots$
> $\text{case}_T$
每组数据格式如下:
> $K\ S_x\ S_y\ T_x\ T_y$
输出格式
输出 $T$ 行,第 $i$ 行输出第 $i$ 组测试数据的答案。
说明/提示
## 限制条件
- $1 \leq T \leq 10^4$
- $2 \leq K \leq 10^{16}$
- $-10^{16} \leq S_x, S_y, T_x, T_y \leq 10^{16}$
- 输入的所有值均为整数
## 样例解释 1
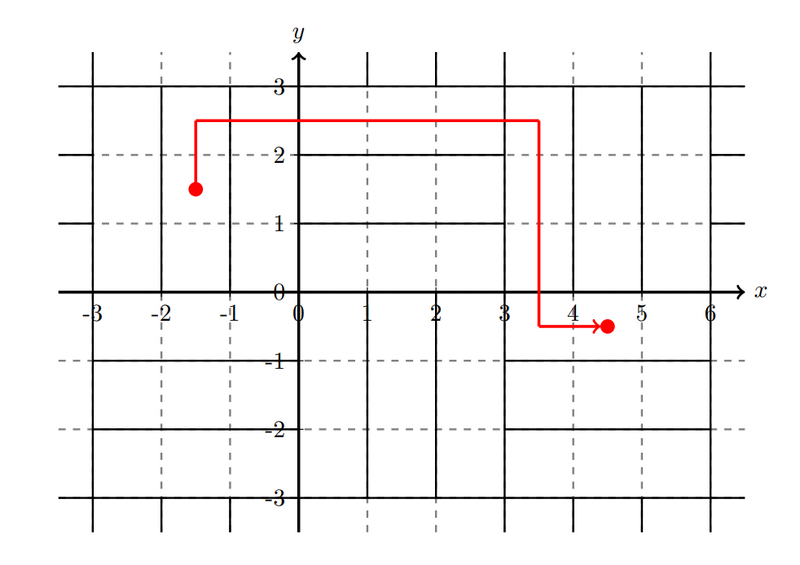
以第 1 组测试数据为例。将与整数三元组 $(i, j, k)$ 对应的瓷砖简称为瓷砖 $(i, j, k)$。$(-1.5, 1.5)$ 包含在瓷砖 $(-1, 0, 1)$ 内,$(4.5, -0.5)$ 包含在瓷砖 $(1, -1, 2)$ 内。例如,可以通过如下移动:瓷砖 $(-1, 0, 1) \to (-1, 0, 2) \to (0, 0, 2) \to (1, 0, 0) \to (1, -1, 2)$,共 4 次移动到达瓷砖 $(1, -1, 2)$。
由 ChatGPT 4.1 翻译