AT_abc384_c [ABC384C] Perfect Standings

Takahashi decided to hold a programming contest. The contest consists of five problems: A, B, C, D, E, with scores $ a $ , $ b $ , $ c $ , $ d $ , $ e $ , respectively. There are $ 31 $ participants, and all of them solved at least one problem. More specifically, for every non-empty subsequence (not necessarily contiguous) of the string `ABCDE`, there is a participant named after that subsequence who solved the problems corresponding to the letters in their name and did not solve the other problems. For example, participant A solved only problem A, and participant BCE solved problems B, C, and E. Print the names of the participants in order of their obtained scores, from the largest to the smallest. The score obtained by a participant is the sum of the scores of the problems they solved. If two participants obtained the same score, print the one whose name is lexicographically smaller first. What does "lexicographically smaller" mean?In short, "lexicographically smaller" refers to the order in which words would appear in a dictionary. More precisely, for distinct strings $ S,T $ consisting of uppercase English letters, $ S $ is lexicographically smaller than $ T $ if either of the following conditions holds: - The length $ |S| $ of $ S $ is less than the length of $ T $ , and the first $ |S| $ characters of $ T $ match $ S $ . - There exists an integer $ 1\leq i\leq\min\{ |S|,|T|\} $ that satisfy both of the following two conditions: - For every integer $ j $ with $ 1\leq j\lt i $ , the $ j $ -th character of $ S $ equals the $ j $ -th character of $ T $ . - The $ i $ -th character of $ S $ is alphabetically smaller than the $ i $ -th character of $ T $ . For example, if $ S= $ `AB` and $ T= $ `ABC`, the first condition holds, so $ S $ is lexicographically smaller than $ T $ . If $ S= $ `ABD` and $ T= $ `ACD`, the second condition holds for $ i=2 $ , so $ S $ is lexicographically smaller than $ T $ .

The input is given from Standard Input in the following format: > $ a $ $ b $ $ c $ $ d $ $ e $

Print $ 31 $ lines. The $ i $ -th line $ (1\leq i\leq 31) $ should contain the name of the participant who obtained the $ i $ -th highest score. If multiple participants have the same score, print them in lexicographical order.

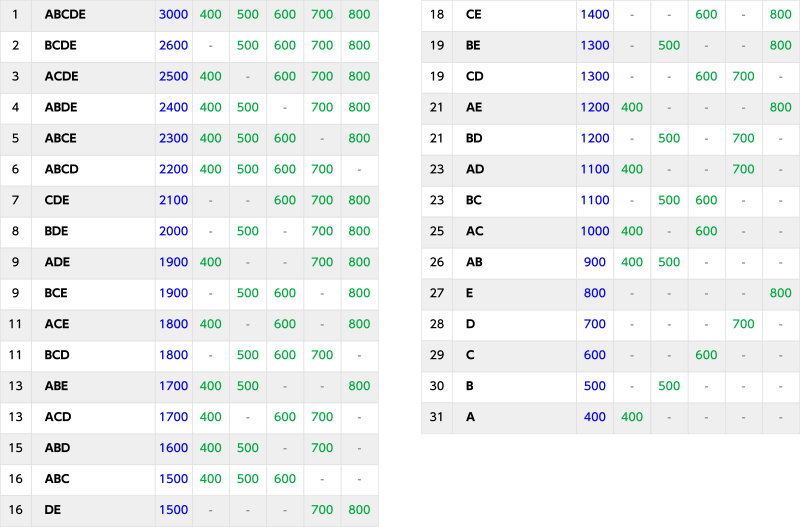
### Sample Explanation 1 The score of each participant is as follows:  For example, ADE and BCE obtained the same score, and ADE is lexicographically smaller, so print ADE before BCE. ### Constraints - $ 100\leq a\leq b\leq c\leq d\leq e\leq 2718 $ - All input values are integers.