AT_abc384_e [ABC384E] Takahashi is Slime 2

縦 $ H $ 行横 $ W $ 列のマス目があります。 上から $ i $ 行目 $ (1\leq i\leq H) $ 、左から $ j $ 列目 $ (1\leq j\leq W) $ のマスをマス $ (i,j) $ と呼ぶことにします。 はじめ、マス $ (i,j) $ には強さ $ S _ {i,j} $ のスライムがおり、マス $ (P,Q) $ にいるスライムが高橋くんです。 高橋くんが以下の行動を好きな回数（ $ 0 $ 回でもよい）行ったあとの、高橋くんの強さとしてありえる最大値を求めてください。 - 高橋くんに隣接するスライムのうち、強さが高橋くんの強さの $ \dfrac1X $ 倍**未満**のものを選んで吸収する。 その結果、吸収されたスライムは消滅し、高橋君の強さは吸収したスライムの強さだけ増加する。 上記の行動の際、スライムが吸収され消滅したことで生じた隙間は直ちに高橋くんによって埋められ、消滅したスライムに隣接していたスライム（それらが存在すれば）は新たに高橋くんと隣接します（入出力例１の説明も参照してください）。

入力は以下の形式で標準入力から与えられる。 > $ H $ $ W $ $ X $ $ P $ $ Q $ $ S _ {1,1} $ $ S _ {1,2} $ $ \ldots $ $ S _ {1,W} $ $ S _ {2,1} $ $ S _ {2,2} $ $ \ldots $ $ S _ {2,W} $ $ \vdots $ $ S _ {H,1} $ $ S _ {H,2} $ $ \ldots $ $ S _ {H,W} $

高橋くんが行動を行ったあとの高橋くんの強さとしてありえる最大値を出力せよ。

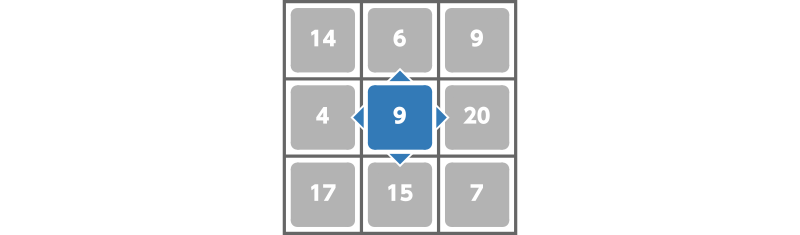
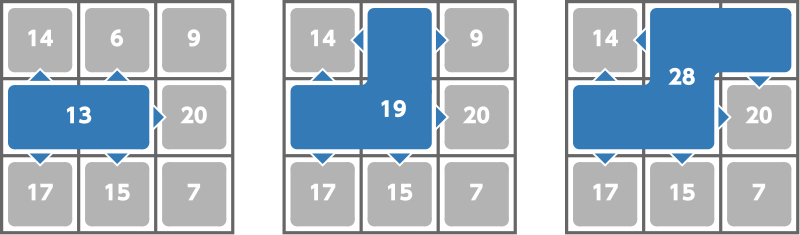
### Sample Explanation 1 はじめ、それぞれのマスにいるスライムの強さは以下の図のようになっています。  例えば、高橋くんは次のように行動を行うことができます。  - マス $ (2,1) $ にいるスライムを吸収する。高橋くんの強さは $ 9+4=13 $ となり、新たにマス $ (1,1) $ のスライムとマス $ (3,1) $ のスライムが高橋くんと隣接する。 - マス $ (1,2) $ にいるスライムを吸収する。高橋くんの強さは $ 13+6=19 $ となり、新たにマス $ (1,3) $ のスライムが高橋くんと隣接する。 - マス $ (1,3) $ にいるスライムを吸収する。高橋くんの強さは $ 19+9=28 $ となる。 以上の行動を行ったあと、高橋くんの強さは $ 28 $ となります。 高橋くんがどのように行動を行っても、高橋くんの強さを $ 28 $ より大きくすることはできないため、`28` を出力してください。 高橋くんの強さの $ \dfrac12 $ 倍未満のスライムしか吸収できないことに注意してください。 例えば、上図の右側の状態からマス $ (1,1) $ にいるスライムを吸収することはできません。 ### Sample Explanation 2 高橋くんはどのスライムも吸収できません。 ### Constraints - $ 1\leq H,W\leq500 $ - $ 1\leq P\leq H $ - $ 1\leq Q\leq W $ - $ 1\leq X\leq10^9 $ - $ 1\leq S _ {i,j}\leq10^{12} $ - 入力はすべて整数