AT_abc385_b [ABC385B] Santa Claus 1

There is a grid with $ H $ rows and $ W $ columns. Let $ (i,j) $ denote the cell at the $ i $ -th row from the top and the $ j $ -th column from the left. If $ S_{i,j} $ is `#`, the cell $ (i,j) $ is impassable; if it is `.`, the cell is passable and contains no house; if it is `@`, the cell is passable and contains a house. Initially, Santa Claus is in cell $ (X,Y) $ . He will act according to the string $ T $ as follows. - Let $ |T| $ be the length of the string $ T $ . For $ i=1,2,\ldots,|T| $ , he moves as follows. - Let $ (x,y) $ be the cell he is currently in. - If $ T_i $ is `U` and cell $ (x-1,y) $ is passable, move to cell $ (x-1,y) $ . - If $ T_i $ is `D` and cell $ (x+1,y) $ is passable, move to cell $ (x+1,y) $ . - If $ T_i $ is `L` and cell $ (x,y-1) $ is passable, move to cell $ (x,y-1) $ . - If $ T_i $ is `R` and cell $ (x,y+1) $ is passable, move to cell $ (x,y+1) $ . - Otherwise, stay in cell $ (x,y) $ . Find the cell where he is after completing all actions, and the number of distinct houses that he passed through or arrived at during his actions. If the same house is passed multiple times, it is only counted once.

The Input is given from Standard Input in the following format: > $ H $ $ W $ $ X $ $ Y $ $ S_{1,1}S_{1,2}\ldots S_{1,W} $ $ \dots $ $ S_{H,1}S_{H,2}\ldots S_{H,W} $ $ T $

Let $ (X,Y) $ be the cell where he is after completing all actions, and $ C $ be the number of distinct houses he passed through or arrived at during his actions. Print $ X,Y,C $ in this order separated by spaces.

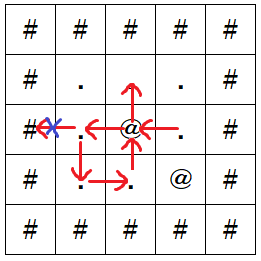
### Sample Explanation 1 Santa Claus behaves as follows:  - $ T_1= $ `L`, so he moves from $ (3,4) $ to $ (3,3) $ . A house is passed. - $ T_2= $ `L`, so he moves from $ (3,3) $ to $ (3,2) $ . - $ T_3= $ `L`, but cell $ (3,1) $ is impassable, so he stays at $ (3,2) $ . - $ T_4= $ `D`, so he moves from $ (3,2) $ to $ (4,2) $ . - $ T_5= $ `R`, so he moves from $ (4,2) $ to $ (4,3) $ . - $ T_6= $ `U`, so he moves from $ (4,3) $ to $ (3,3) $ . A house is passed, but it has already been passed. - $ T_7= $ `U`, so he moves from $ (3,3) $ to $ (2,3) $ . The number of houses he passed or arrived during his actions is $ 1 $ . ### Constraints - $ 3 \leq H,W \leq 100 $ - $ 1 \leq X \leq H $ - $ 1 \leq Y \leq W $ - All given numbers are integers. - Each $ S_{i,j} $ is one of `#`, `.`, `@`. - $ S_{i,1} $ and $ S_{i,W} $ are `#` for every $ 1 \leq i \leq H $ . - $ S_{1,j} $ and $ S_{H,j} $ are `#` for every $ 1 \leq j \leq W $ . - $ S_{X,Y}= $ `.` - $ T $ is a string of length at least $ 1 $ and at most $ 10^4 $ , consisting of `U`, `D`, `L`, `R`.