AT_abc385_b [ABC385B] Santa Claus 1

縦 $ H $ 行横 $ W $ 列のマス目があります。上から $ i $ 行目、左から $ j $ 列目のマスをマス $ (i,j) $ と表します。 マス $ (i,j) $ は $ S_{i,j} $ が `#` のとき通行不可能、`.` のとき通行可能であり家が建っていない、`@` のとき通行可能であり家が建っていることを表します。 最初、マス $ (X,Y) $ にサンタクロースがいます。サンタクロースは文字列 $ T $ に従って以下の行動を行います。 - 文字列 $ T $ の長さを $ |T| $ とする。 $ i=1,2,\ldots,|T| $ の順に以下のように移動する。 - 現在サンタクロースがいるマスを $ (x,y) $ とする。 - $ T_i $ が `U` かつマス $ (x-1,y) $ が通行可能ならマス $ (x-1,y) $ に移動する。 - $ T_i $ が `D` かつマス $ (x+1,y) $ が通行可能ならマス $ (x+1,y) $ に移動する。 - $ T_i $ が `L` かつマス $ (x,y-1) $ が通行可能ならマス $ (x,y-1) $ に移動する。 - $ T_i $ が `R` かつマス $ (x,y+1) $ が通行可能ならマス $ (x,y+1) $ に移動する。 - それ以外の場合、マス $ (x,y) $ に留まる。 行動を終えたあとにサンタクロースがいるマスと、行動により通過または到達した家の数を求めてください。ただし、同じ家を複数回通過または到達してもそれらは重複して数えません。

入力は以下の形式で標準入力から与えられる。 > $ H $ $ W $ $ X $ $ Y $ $ S_{1,1}S_{1,2}\ldots S_{1,W} $ $ \dots $ $ S_{H,1}S_{H,2}\ldots S_{H,W} $ $ T $

行動を終えたあとサンタクロースがいるマスを $ (X,Y) $ 、行動により通過または到達した家の数を $ C $ とするとき、 $ X,Y,C $ をこの順に空白区切りで出力せよ。

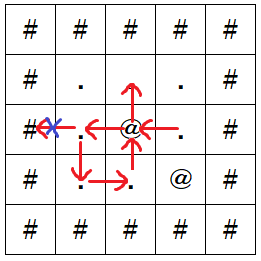
### Sample Explanation 1 サンタクロースは以下のように行動します。  - $ T_1= $ `L` なのでマス $ (3,4) $ からマス $ (3,3) $ に移動する。これにより家を通過する。 - $ T_2= $ `L` なのでマス $ (3,3) $ からマス $ (3,2) $ に移動する。 - $ T_3= $ `L` だがマス $ (3,1) $ は通行不可能なので、マス $ (3,2) $ に留まる。 - $ T_4= $ `D` なのでマス $ (3,2) $ からマス $ (4,2) $ に移動する。 - $ T_5= $ `R` なのでマス $ (4,2) $ からマス $ (4,3) $ に移動する。 - $ T_6= $ `U` なのでマス $ (4,3) $ からマス $ (3,3) $ に移動する。これにより家を通過するが、この家はすでに通過したことがある家である。 - $ T_7= $ `U` なのでマス $ (3,3) $ からマス $ (2,3) $ に移動する。 行動により通過または到達した家の数は $ 1 $ です。 ### Constraints - $ 3 \leq H,W \leq 100 $ - $ 1 \leq X \leq H $ - $ 1 \leq Y \leq W $ - 与えられる数値は全て整数である - $ S_{i,j} $ は `#`, `.`, `@` のいずれか - 全ての $ 1 \leq i \leq H $ について $ S_{i,1},S_{i,W} $ は `#` - 全ての $ 1 \leq j \leq W $ について $ S_{1,j},S_{H,j} $ は `#` - $ S_{X,Y}= $ `.` - $ T $ は `U`, `D`, `L`, `R` のいずれかからなる長さ $ 1 $ 以上 $ 10^4 $ 以下の文字列