AT_abc385_d [ABC385D] Santa Claus 2

There are $ N $ houses at points $ (X_1,Y_1),\ldots,(X_N,Y_N) $ on a two-dimensional plane. Initially, Santa Claus is at point $ (S_x,S_y) $ . He will act according to the sequence $ (D_1,C_1),\ldots,(D_M,C_M) $ as follows: - For $ i=1,2,\ldots,M $ in order, he moves as follows: - Let $ (x,y) $ be the point where he currently is. - If $ D_i $ is `U`, move in a straight line from $ (x,y) $ to $ (x,y+C_i) $ . - If $ D_i $ is `D`, move in a straight line from $ (x,y) $ to $ (x,y-C_i) $ . - If $ D_i $ is `L`, move in a straight line from $ (x,y) $ to $ (x-C_i,y) $ . - If $ D_i $ is `R`, move in a straight line from $ (x,y) $ to $ (x+C_i,y) $ . Find the point where he is after completing all actions, and the number of distinct houses he passed through or arrived at during his actions. If the same house is passed multiple times, it is only counted once.

The input is given from Standard Input in the following format: > $ N $ $ M $ $ S_x $ $ S_y $ $ X_1 $ $ Y_1 $ $ \vdots $ $ X_N $ $ Y_N $ $ D_1 $ $ C_1 $ $ \vdots $ $ D_M $ $ C_M $

Let $ (X,Y) $ be the point where he is after completing all actions, and $ C $ be the number of distinct houses passed through or arrived at. Print $ X,Y,C $ in this order separated by spaces.

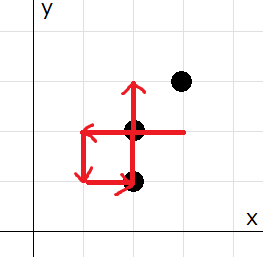
### Sample Explanation 1 Santa Claus behaves as follows:  - $ D_1= $ `L`, so he moves from $ (3,2) $ to $ (3-2,2) $ in a straight line. During this, he passes through the house at $ (2,2) $ . - $ D_2= $ `D`, so he moves from $ (1,2) $ to $ (1,2-1) $ in a straight line. - $ D_3= $ `R`, so he moves from $ (1,1) $ to $ (1+1,1) $ in a straight line. During this, he passes through the house at $ (2,1) $ . - $ D_4= $ `U`, so he moves from $ (2,1) $ to $ (2,1+2) $ in a straight line. During this, he passes through the house at $ (2,2) $ , but it has already been passed. The number of houses he passed or arrived during his actions is $ 2 $ . ### Sample Explanation 2 Be careful with overflow. ### Constraints - $ 1 \leq N \leq 2\times 10^5 $ - $ 1 \leq M \leq 2\times 10^5 $ - $ -10^9 \leq X_i,Y_i \leq 10^9 $ - The pairs $ (X_i,Y_i) $ are distinct. - $ -10^9 \leq S_x,S_y \leq 10^9 $ - There is no house at $ (S_x,S_y) $ . - Each $ D_i $ is one of `U`, `D`, `L`, `R`. - $ 1 \leq C_i \leq 10^9 $ - All input numbers are integers.