AT_abc385_d [ABC385D] Santa Claus 2

在二次元平面上有 $N$ 个点 $(X_1,Y_1),\ldots,(X_N,Y_N)$ 建有房子。 最初，圣诞老人在点 $(S_x,S_y)$。圣诞老人将按照序列 $(D_1,C_1),\ldots,(D_M,C_M)$ 进行以下行动： - 对于 $i=1,2,\ldots,M$，按顺序进行以下移动： - 设 $(x,y)$ 为他当前所在的点。 - 如果 $D_i$ 是 `U`，则从 $(x,y)$ 沿直线移动到 $(x,y+C_i)$。 - 如果 $D_i$ 是 `D`，则从 $(x,y)$ 沿直线移动到 $(x,y-C_i)$。 - 如果 $D_i$ 是 `L`，则从 $(x,y)$ 沿直线移动到 $(x-C_i,y)$。 - 如果 $D_i$ 是 `R`，则从 $(x,y)$ 沿直线移动到 $(x+C_i,y)$。 请找出他完成所有行动后所在的点，以及他在行动过程中经过或到达的不同房子的数量。如果多次经过同一个房子，只计数一次。

输入从标准输入按以下格式给出： > $N$ $M$ $S_x$ $S_y$ $X_1$ $Y_1$ $\dots$ $X_N$ $Y_N$ $D_1$ $C_1$ $\dots$ $D_M$ $C_M$

设 $(X,Y)$ 为他完成所有行动后所在的点，$C$ 为他在行动过程中经过或到达的不同房子的数量。按顺序输出用空格分隔的 $X$、$Y$、$C$。

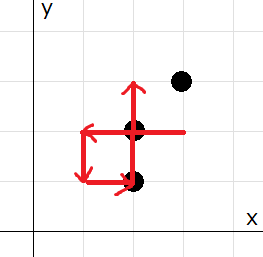
- $1 \leq N \leq 2\times 10^5$ - $1 \leq M \leq 2\times 10^5$ - $-10^9 \leq X_i,Y_i \leq 10^9$ - $(X_i,Y_i)$ 互不相同 - $-10^9 \leq S_x,S_y \leq 10^9$ - 点 $(S_x,S_y)$ 没有房子 - 每个 $D_i$ 是 `U`、`D`、`L`、`R` 之一 - $1 \leq C_i \leq 10^9$ - 所有给定数字均为整数 **【样例 #1 解释】** 圣诞老人的行动如下图所示：  - $D_1=$ `L`，所以他从 $(3,2)$ 直线移动到 $(3-2,2)$。在此期间，他经过 $(2,2)$ 处的房子。 - $D_2=$ `D`，所以他从 $(1,2)$ 直线移动到 $(1,2-1)$。 - $D_3=$ `R`，所以他从 $(1,1)$ 直线移动到 $(1+1,1)$。在此期间，他经过 $(2,1)$ 处的房子。 - $D_4=$ `U`，所以他从 $(2,1)$ 直线移动到 $(2,1+2)$。在此期间，他经过 $(2,2)$ 处的房子，但该房子已经被经过。 他在行动期间经过或到达的房子数量为 $2$。 **【样例 #2 解释】** 小心溢出。