AT_abc385_e [ABC385E] Snowflake Tree

A "Snowflake Tree" is defined as a tree that can be generated by the following procedure: 1. Choose positive integers $ x,y $ . 2. Prepare one vertex. 3. Prepare $ x $ more vertices, and connect each of them to the vertex prepared in step 2. 4. For each of the $ x $ vertices prepared in step 3, attach $ y $ leaves to it. The figure below shows a Snowflake Tree with $ x=4,y=2 $ . The vertices prepared in steps 2, 3, 4 are shown in red, blue, and green, respectively.  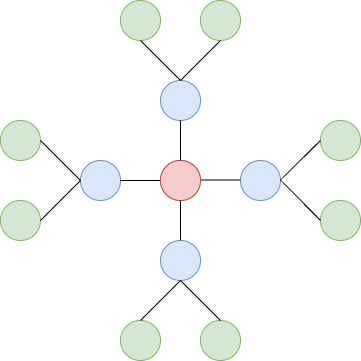You are given a tree $ T $ with $ N $ vertices. The vertices are numbered $ 1 $ to $ N $ , and the $ i $ -th edge $ (i=1,2,\dots,N-1) $ connects vertices $ u_i $ and $ v_i $ . Consider deleting zero or more vertices of $ T $ and the edges adjacent to them so that the remaining graph becomes a single Snowflake Tree. Find the minimum number of vertices that must be deleted. Under the constraints of this problem, it is always possible to transform $ T $ into a Snowflake Tree.

The input is given from Standard Input in the following format: > $ N $ $ u_1 $ $ v_1 $ $ u_2 $ $ v_2 $ $ \vdots $ $ u_{N-1} $ $ v_{N-1} $

Print the answer.

### Sample Explanation 1 By deleting vertex $ 8 $ , the given tree can be transformed into a Snowflake Tree with $ x=2,y=2 $ . ### Sample Explanation 2 The given tree is already a Snowflake Tree with $ x=1,y=1 $ . ### Constraints - $ 3 \leq N \leq 3 \times 10^5 $ - $ 1 \leq u_i < v_i \leq N $ - The given graph is a tree. - All input values are integers.