AT_abc385_e [ABC385E] Snowflake Tree

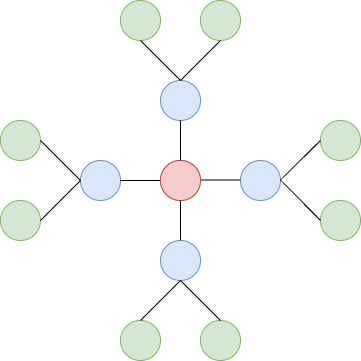
「**ユ木**」を、以下の手順で生成することができる木と定義します。 1. 正整数 $ x,y $ を選ぶ 2. 頂点を $ 1 $ つ用意する 3. 別に $ x $ 個の頂点を用意し、それぞれを手順 $ 2 $ で用意した頂点と辺で結ぶ 4. 手順 $ 3 $ で用意した $ x $ 個の頂点それぞれに、 $ y $ 個の葉をつける $ x=4,y=2 $ のユ木を下図に示します。手順 $ 2,3,4 $ で用意される頂点をそれぞれ赤、青、緑で示しています。  $ N $ 頂点の木 $ T $ が与えられます。頂点には $ 1 $ から $ N $ の番号が付けられており、 $ i\;(=1,2,\dots,N-1) $ 番目の辺は頂点 $ u_i $ と頂点 $ v_i $ を結びます。 $ T $ の $ 0 $ 個以上の頂点とそれに隣接する辺を削除して $ 1 $ つのユ木にするとき、削除する頂点数の最小値を求めてください。なお、本問題の制約下で、 $ T $ をかならずユ木にすることができます。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ u_1 $ $ v_1 $ $ u_2 $ $ v_2 $ $ \vdots $ $ u_{N-1} $ $ v_{N-1} $

答えを出力せよ。

### Sample Explanation 1 頂点 $ 8 $ を削除することで、与えられた木を $ x=2,y=2 $ のユ木にすることができます。 ### Sample Explanation 2 与えられた木はすでに $ x=1,y=1 $ のユ木です。 ### Constraints - $ 3 \leq N \leq 3 \times 10^5 $ - $ 1 \leq u_i < v_i \leq N $ - 与えられるグラフは木である - 入力はすべて整数