AT_abc385_f [ABC385F] Visible Buildings

There are $ N $ buildings numbered $ 1 $ to $ N $ on a number line. Building $ i $ is at coordinate $ X_i $ and has height $ H_i $ . The size in directions other than height is negligible. From a point $ P $ with coordinate $ x $ and height $ h $ , building $ i $ is considered visible if there exists a point $ Q $ on building $ i $ such that the line segment $ PQ $ does not intersect with any other building. Find the maximum height at coordinate $ 0 $ from which it is not possible to see all buildings. Height must be non-negative; if it is possible to see all buildings at height $ 0 $ at coordinate $ 0 $ , report `-1` instead.

The input is given from Standard Input in the following format: > $ N $ $ X_1 $ $ H_1 $ $ \vdots $ $ X_N $ $ H_N $

If it is possible to see all buildings from coordinate $ 0 $ and height $ 0 $ , print `-1`. Otherwise, print the maximum height at coordinate $ 0 $ from which it is not possible to see all buildings. Answers with an absolute or relative error of at most $ 10^{-9} $ from the true answer will be considered correct.

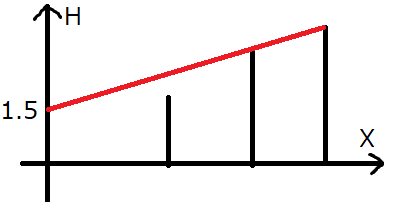
### Sample Explanation 1 From coordinate $ 0 $ and height $ 1.5 $ , building $ 3 $ cannot be seen. If the height is even slightly greater than $ 1.5 $ , all buildings including building $ 3 $ can be seen. Thus, the answer is $ 1.5 $ .  ### Sample Explanation 2 Note that `-1.000` or similar outputs would be considered incorrect. ### Constraints - $ 1 \leq N \leq 2 \times 10^5 $ - $ 1 \leq X_1 < \dots < X_N \leq 10^9 $ - $ 1 \leq H_i \leq 10^9 $ - All input values are integers.