AT_abc385_f [ABC385F] Visible Buildings

$ 1 $ から $ N $ の番号がついた $ N $ 棟のビルが数直線上に建っています。 ビル $ i $ は座標 $ X_i $ にあり、高さは $ H_i $ です。ビルの高さ方向以外の大きさは無視できるものとします。 座標 $ x $ の高さ $ h $ の地点 $ P $ からビル $ i $ が見えるとは、ビル $ i $ 上のある点 $ Q $ であって、線分 $ PQ $ が他のビルと共有点を持たないものが存在することと定めます。 座標 $ 0 $ から全てのビルを見ることができない高さの最大値を求めてください。ただし、高さは非負の値を取るとし、高さ $ 0 $ で全てのビルを見ることができる場合はかわりに `-1` と答えてください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ X_1 $ $ H_1 $ $ \vdots $ $ X_N $ $ H_N $

座標 $ 0 $ 、高さ $ 0 $ の地点から全てのビルを見ることができる場合は `-1` と出力せよ。 そうでないとき、座標 $ 0 $ から全てのビルを見ることができない高さの最大値を出力せよ。真の解との絶対誤差または相対誤差が $ 10^{-9} $ 以下のとき正解と判定される。

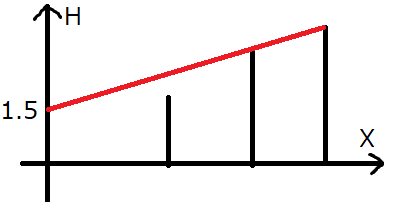
### Sample Explanation 1 座標 $ 0 $ 高さ $ 1.5 $ の位置ではビル $ 3 $ を見ることができません。高さが $ 1.5 $ より僅かでも高ければビル $ 3 $ を含む全てのビルを見ることができるため、答えは $ 1.5 $ です。  ### Sample Explanation 2 `-1.000` などの出力では不正解となることに注意してください。 ### Constraints - $ 1 \leq N \leq 2 \times 10^5 $ - $ 1 \leq X_1 < \dots < X_N \leq 10^9 $ - $ 1 \leq H_i \leq 10^9 $ - 入力は全て整数である