AT_abc385_f [ABC385F] Visible Buildings

在数轴上有编号从 $1$ 到 $N$ 的建筑物。第 $i$ 个建筑物位于坐标 $X_i$ 处，高度为 $H_i$。除了高度外的其他方向的尺寸可以忽略不计。 从坐标为 $x$ 且高度为 $h$ 的点 $P$ 看，如果存在建筑物 $i$ 上的某个点 $Q$，使得线段 $PQ$ 不与任何其他建筑物相交，则认为该建筑物是可见的。 请找出在坐标 $0$ 处的最大高度，使得在该高度无法看到所有建筑物。高度必须是非负的；如果在坐标 $0$ 处的高度 $0$ 就能看到所有建筑物，则输出 `-1`。

输入从标准输入按以下格式给出： > $N$ $X_1$ $H_1$ $\vdots$ $X_N$ $H_N$

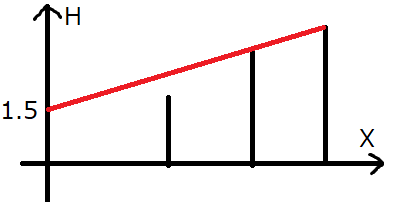
如果在坐标 $0$ 处高度 $0$ 就能看到所有建筑物，输出 `-1`。否则，输出在坐标 $0$ 处无法看到所有建筑物的最大高度。答案与真实值的绝对误差或相对误差在 $10^{-9}$ 以内的解答将被视为正确。 **【样例解释 $\bm 1$】** 从坐标 $0$ 处高度 $1.5$ 的位置看，无法看到建筑物 $3$。如果高度比 $1.5$ 稍高一点，就能看到包括建筑物 $3$ 在内的所有建筑物。因此，答案是 $1.5$。  **【样例解释 $\bm 2$】** 注意，输出 `-1.000` 或类似的格式将被视为错误答案。

- $1 \leq N \leq 2 \times 10^5$ - $1 \leq X_1 < \dots < X_N \leq 10^9$ - $1 \leq H_i \leq 10^9$ - 所有输入值均为整数。