AT_abc386_g [ABC386G] Many MST

You are given positive integers $ N $ and $ M $ . Consider a weighted complete graph with $ N $ vertices labeled from $ 1 $ to $ N $ , where the weight of each edge is an integer between $ 1 $ and $ M $ , inclusive. There are $ M^{N(N-1)/2} $ such graphs. For each of them, consider the sum of the weights of the edges included in its Minimum Spanning Tree. What is the total of these sums? Print the result modulo $ 998244353 $ .

The input is given from Standard Input in the following format: > $ N $ $ M $

Print the answer.

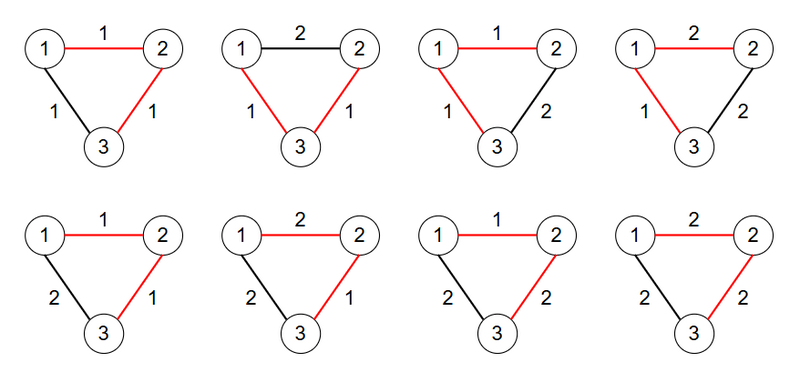
### Sample Explanation 1 Here are eight complete graphs with three vertices where edge weights are $ 1 $ or $ 2 $ . The edges in each graph’s MST are highlighted in red in the figure below.  The sums of the MST edges for these graphs are $ 2,2,2,3,2,3,3,4 $ , so the total is $ 2+2+2+3+2+3+3+4=21 $ . ### Constraints - $ 2 \le N \le 500 $ - $ 1 \le M \le 500 $ - All input values are integers.