AT_abc386_g [ABC386G] Many MST
Description
正整数 $ N,M $ が与えられます。頂点に $ 1 $ から $ N $ までの番号がつけられている $ N $ 頂点の重み付き完全グラフであって各辺の重みが $ 1 $ 以上 $ M $ 以下の整数であるようなものは $ M^{N(N-1)/2} $ 通りありますが、それぞれについて最小全域木に含まれる辺の重みの和を求めたとき、それらの総和はいくつになりますか?総和を $ 998244353 $ で割った余りを出力してください。
Input Format
入力は以下の形式で標準入力から与えられる。
> $ N $ $ M $
Output Format
答えを出力せよ。
Explanation/Hint
### Sample Explanation 1
辺の重みが $ 1 $ または $ 2 $ である $ 3 $ 頂点の重み付き完全グラフは以下の $ 8 $ つあります。それぞれの完全グラフについて、最小全域木に含まれる辺は赤色で塗られています。
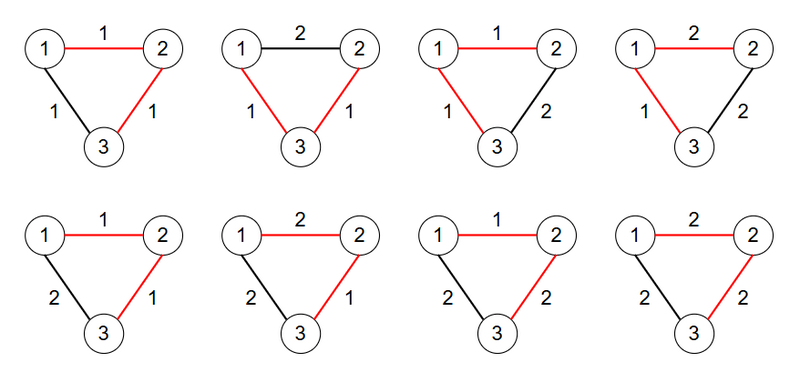
それぞれの完全グラフの最小全域木に含まれる辺の重みの和は $ 2,2,2,3,2,3,3,4 $ であるため、求める答えは $ 2+2+2+3+2+3+3+4=21 $ です。
### Constraints
- $ 2\leq N\leq 500 $
- $ 1\leq M\leq 500 $
- 入力は全て整数