AT_abc387_d [ABC387D] Snaky Walk

You are given a grid with $ H $ rows and $ W $ columns. Let $ (i,j) $ denote the cell at the $ i $ -th row from the top and the $ j $ -th column from the left. Each cell is one of the following: a start cell, a goal cell, an empty cell, or an obstacle cell. This information is described by $ H $ strings $ S_1,S_2,\dots,S_H $ , each of length $ W $ . Specifically, the cell $ (i,j) $ is a start cell if the $ j $ -th character of $ S_i $ is `S`, a goal cell if it is `G`, an empty cell if it is `.`, and an obstacle cell if it is `#`. It is guaranteed that there is exactly one start cell and exactly one goal cell. You are currently on the start cell. Your objective is to reach the goal cell by repeatedly moving to a cell adjacent by an edge to the one you are in. However, you cannot move onto an obstacle cell or move outside the grid, and you must alternate between moving vertically and moving horizontally each time. (The direction of the first move can be chosen arbitrarily.) Determine if it is possible to reach the goal cell. If it is, find the minimum number of moves required. More formally, check if there exists a sequence of cells $ (i_1,j_1),(i_2,j_2),\dots,(i_k,j_k) $ satisfying all of the following conditions. If such a sequence exists, find the minimum value of $ k-1 $ . - For every $ 1 \leq l \leq k $ , it holds that $ 1 \leq i_l \leq H $ and $ 1 \leq j_l \leq W $ , and $ (i_l,j_l) $ is not an obstacle cell. - $ (i_1,j_1) $ is the start cell. - $ (i_k,j_k) $ is the goal cell. - For every $ 1 \leq l \leq k-1 $ , $ |i_l - i_{l+1}| + |j_l - j_{l+1}| = 1 $ . - For every $ 1 \leq l \leq k-2 $ , if $ i_l \neq i_{l+1} $ , then $ i_{l+1} = i_{l+2} $ . - For every $ 1 \leq l \leq k-2 $ , if $ j_l \neq j_{l+1} $ , then $ j_{l+1} = j_{l+2} $ .

The input is given from Standard Input in the following format: > $ H $ $ W $ $ S_1 $ $ S_2 $ $ \vdots $ $ S_H $

If it is possible to reach the goal cell, print the minimum number of moves. Otherwise, print `-1`.

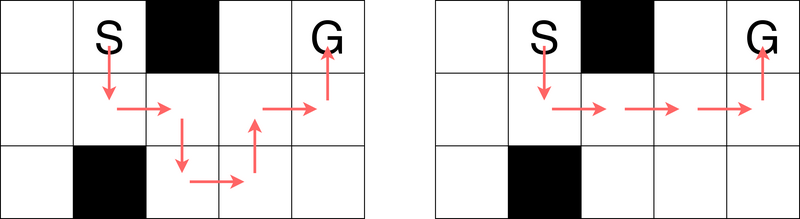
### Sample Explanation 1  As shown in the left figure, you can move as $ (1,2)\rightarrow(2,2)\rightarrow(2,3)\rightarrow(3,3)\rightarrow(3,4)\rightarrow(2,4)\rightarrow(2,5)\rightarrow(1,5) $ , reaching the goal cell in $ 7 $ moves. It is impossible in $ 6 $ moves or fewer, so the answer is $ 7 $ . Note that you cannot take a path that moves horizontally (or vertically) consecutively without alternating as shown in the right figure. ### Sample Explanation 2 It is not possible to reach the goal cell. ### Constraints - $ 1 \leq H,W \leq 1000 $ - $ H $ and $ W $ are integers. - Each $ S_i $ is a string of length $ W $ consisting of `S`, `G`, `.`, `#`. - There is exactly one start cell and exactly one goal cell.