AT_abc387_d [ABC387D] Snaky Walk

$ H $ 行 $ W $ 列のグリッドがあります。 上から $ i $ 行目、左から $ j $ 列目のマスを $ (i,j) $ と表記します。 各マスはスタートマス・ゴールマス・空きマス・障害物マスのいずれかであり、その情報は $ H $ 個の長さ $ W $ の文字列 $ S_1,S_2,\dots,S_H $ によって表されます。 具体的には、マス $ (i,j) $ は $ S_i $ の $ j $ 文字目が `S` であるときスタートマス、`G` であるときゴールマス、`.` であるとき空きマス、`#` であるとき障害物マスです。 ここで、スタートマスとゴールマスはちょうど $ 1 $ つずつ存在することが保証されます。 あなたは今スタートマスにいます。 あなたの目標は、今いるマスと辺で隣接するマスに移動することを繰り返してゴールマスへ行くことです。 ただし、障害物マスやグリッドの外に移動することはできず、また縦移動と横移動を $ 1 $ 回ずつ交互に行わなければなりません。（最初の移動の向きは任意です。） ゴールマスへ行くことが可能であるか判定し、可能ならば移動回数の最小値を求めてください。 より形式的には、以下の条件をすべて満たすマスの列 $ (i_1,j_1),(i_2,j_2),\dots,(i_k,j_k) $ が存在するか判定し、存在するならば $ k-1 $ の最小値を求めてください。 - すべての $ 1\leq l\leq k $ について、 $ 1\leq i_l\leq H $ かつ $ 1\leq j_l\leq W $ であり、 $ (i_l,j_l) $ は障害物マスでない - $ (i_1,j_1) $ はスタートマス - $ (i_k,j_k) $ はゴールマス - すべての $ 1\leq l\leq k-1 $ について、 $ |i_l-i_{l+1}|+|j_l-j_{l+1}|=1 $ - すべての $ 1\leq l\leq k-2 $ について、 $ i_l\neq i_{l+1} $ ならば $ i_{l+1}=i_{l+2} $ - すべての $ 1\leq l\leq k-2 $ について、 $ j_l\neq j_{l+1} $ ならば $ j_{l+1}=j_{l+2} $

入力は以下の形式で標準入力から与えられる。 > $ H $ $ W $ $ S_1 $ $ S_2 $ $ \vdots $ $ S_H $

ゴールマスへ行くことが可能ならば移動回数の最小値を、不可能ならば `-1` を出力せよ。

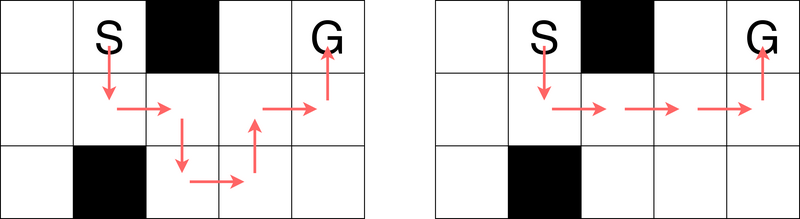
### Sample Explanation 1  左図のように $ (1,2)\rightarrow(2,2)\rightarrow(2,3)\rightarrow(3,3)\rightarrow(3,4)\rightarrow(2,4)\rightarrow(2,5)\rightarrow(1,5) $ と移動することで、 $ 7 $ 回の移動でゴールマスへ行くことができます。 $ 6 $ 回以下の移動でゴールマスへ行くことはできないので、答えは $ 7 $ です。 右図のように横移動を連続で行う経路（あるいは縦移動を連続で行う経路）はとれないことに注意してください。 ### Sample Explanation 2 ゴールマスへ行くことはできません。 ### Constraints - $ 1\leq H,W \leq 1000 $ - $ H,W $ は整数 - $ S_i $ は `S`, `G`, `.`, `#` からなる長さ $ W $ の文字列 - スタートマスとゴールマスはちょうど $ 1 $ つずつ存在する