AT_abc387_d [ABC387D] Snaky Walk

有一个 $H$ 行 $W$ 列的网格。从上往下第 $i$ 行、从左往右第 $j$ 列的单元格记为 $(i,j)$。 每个单元格是起点、终点、空单元格或障碍物，这些信息由 $H$ 个长度为 $W$ 的字符串 $S_1,S_2,\dots,S_H$ 表示。具体来说，当 $S_i$ 的第 $j$ 个字符是 `S` 时，单元格 $(i,j)$ 是起点；是 `G` 时是终点；是 `.` 时是空单元格；是 `#` 时是障碍物。保证起点和终点各恰好存在一个。 你现在位于起点。你的目标是通过重复移动到当前单元格边相邻的单元格，最终到达终点。但有以下限制：不能移动到障碍物或网格外，且必须交替进行纵向移动和横向移动（首次移动方向可任选）。 请判断能否到达终点，若可能则求出移动次数的最小值。 更形式化地说，请判断是否存在满足以下所有条件的单元格序列 $(i_1,j_1),(i_2,j_2),\dots,(i_k,j_k)$，若存在则求 $k-1$ 的最小值： - 对所有 $1 \leq l \leq k$，满足 $1 \leq i_l \leq H$ 且 $1 \leq j_l \leq W$，且 $(i_l,j_l)$ 不是障碍物 - $(i_1,j_1)$ 是起点 - $(i_k,j_k)$ 是终点 - 对所有 $1 \leq l \leq k-1$，满足 $|i_l - i_{l+1}| + |j_l - j_{l+1}| = 1$ - 对所有 $1 \leq l \leq k-2$，若 $i_l \neq i_{l+1}$，则 $i_{l+1} = i_{l+2}$ - 对所有 $1 \leq l \leq k-2$，若 $j_l \neq j_{l+1}$，则 $j_{l+1} = j_{l+2}$

输入通过标准输入给出，格式如下： > $H$ $W$ > $S_1$ > $S_2$ > $\vdots$ > $S_H$

若可以到达终点，输出移动次数的最小值；否则输出 `-1`。

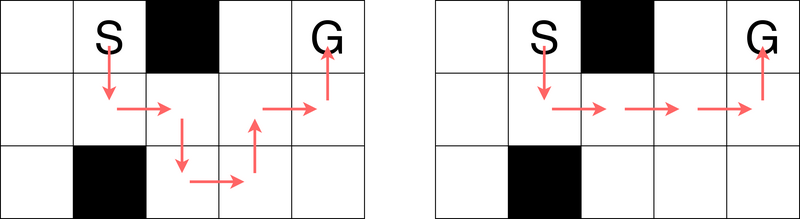
### 约束条件 - $1 \leq H, W \leq 1000$ - $H, W$ 是整数 - $S_i$ 是由 `S`、`G`、`.`、`#` 组成的长度为 $W$ 的字符串 - 起点和终点各恰好存在一个 ### 样例解释 1  按照左图的路径 $(1,2) \rightarrow (2,2) \rightarrow (2,3) \rightarrow (3,3) \rightarrow (3,4) \rightarrow (2,4) \rightarrow (2,5) \rightarrow (1,5)$，可以通过 7 次移动到达终点。无法用 6 次或更少移动到达终点，因此答案是 7。注意右图所示的连续横向移动（或连续纵向移动）路径是不被允许的。 ### 样例解释 2 无法到达终点。 翻译由 DeepSeek R1 完成