AT_abc388_c [ABC388C] Various Kagamimochi

There are $ N $ mochi (rice cakes) arranged in ascending order of size. The size of the $ i $ -th mochi $ (1 \leq i \leq N) $ is $ A_i $ . Given two mochi $ A $ and $ B $ , with sizes $ a $ and $ b $ respectively, you can make one kagamimochi (a stacked rice cake) by placing mochi $ A $ on top of mochi $ B $ if and only if $ a $ is at most half of $ b $ . You choose two mochi out of the $ N $ mochi, and place one on top of the other to form one kagamimochi. Find how many different kinds of kagamimochi can be made. Two kagamimochi are distinguished if at least one of the mochi is different, even if the sizes of the mochi are the same.

The input is given from Standard Input in the following format: > $ N $ $ A_1 $ $ A_2 $ $ \cdots $ $ A_N $

Print the number of different kinds of kagamimochi that can be made.

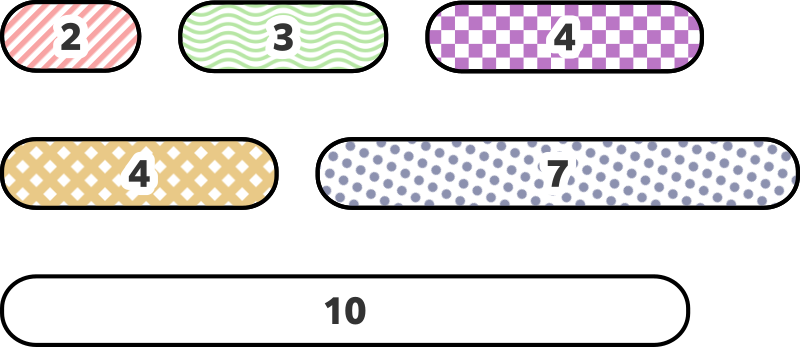
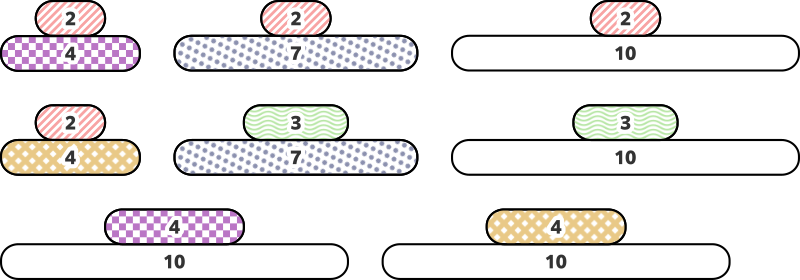
### Sample Explanation 1 The sizes of the given mochi are as follows:  In this case, you can make the following eight kinds of kagamimochi:  Note that there are two kinds of kagamimochi where a mochi of size $ 4 $ is topped by a mochi of size $ 2 $ , and two kinds where a mochi of size $ 10 $ is topped by a mochi of size $ 4 $ . ### Sample Explanation 2 It is possible that you cannot make any kagamimochi. ### Constraints - $ 2 \leq N \leq 5 \times 10^5 $ - $ 1 \leq A_i \leq 10^9 \ (1 \leq i \leq N) $ - $ A_i \leq A_{i+1} \ (1 \leq i < N) $ - All input values are integers.