AT_abc388_c [ABC388C] Various Kagamimochi

$ N $ 個の餅が小さいほうから順に並んでいます。 $ i $ 番目 $ (1\leq i\leq N) $ の餅の大きさは $ A _ i $ です。 $ 2 $ つの餅 $ A,B $ の大きさをそれぞれ $ a,b $ としたとき、 $ a $ が $ b $ の半分以下であるとき、かつそのときに限り、餅 $ A $ を餅 $ B $ の上に乗せて鏡餅を $ 1 $ つ作ることができます。 $ N $ 個の餅から $ 2 $ つの餅を選び、一方をもう一方の上に乗せることで鏡餅を $ 1 $ つ作ります。 何種類の鏡餅を作ることができるか求めてください。 ただし、鏡餅を構成する餅の大きさが同じでも、少なくとも一方が異なる餅であれば別の種類の鏡餅として数えます。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ A _ 1 $ $ A _ 2 $ $ \cdots $ $ A _ N $

作ることができる鏡餅の種類数を出力せよ。

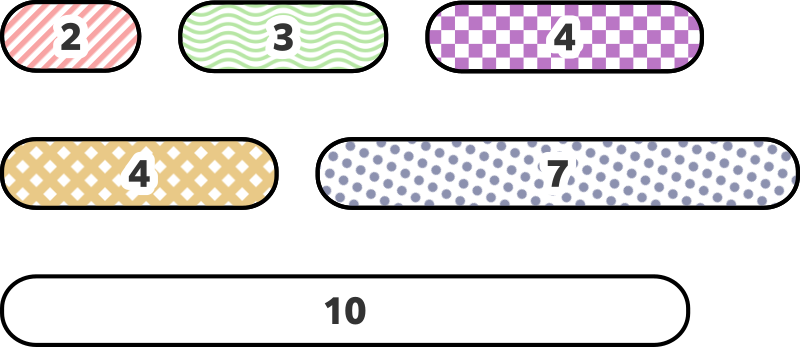
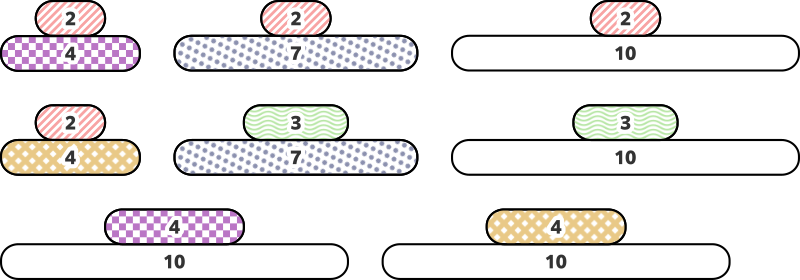
### Sample Explanation 1 与えられた餅の大きさは以下のようになっています。  このとき、以下の $ 8 $ 種類の鏡餅を作ることができます。  大きさ $ 4 $ の餅の上に大きさ $ 2 $ の餅を乗せた鏡餅や、大きさ $ 10 $ の餅の上に大きさ $ 4 $ の餅を乗せた鏡餅は $ 2 $ 種類あることに注意してください。 ### Sample Explanation 2 鏡餅を $ 1 $ 種類も作ることができない場合もあります。 ### Constraints - $ 2\leq N\leq 5\times 10 ^ 5 $ - $ 1\leq A _ i\leq 10 ^ 9\ (1\leq i\leq N) $ - $ A _ i\leq A _ {i+1}\ (1\leq i\lt N) $ - 入力はすべて整数