AT_abc388_e [ABC388E] Simultaneous Kagamimochi

$ N $ 個の餅が小さいほうから順に並んでいます。 $ i $ 番目 $ (1\leq i\leq N) $ の餅の大きさは $ A _ i $ です。 $ 2 $ つの餅 $ A,B $ の大きさをそれぞれ $ a,b $ としたとき、 $ a $ が $ b $ の半分以下であるとき、かつそのときに限り、餅 $ A $ を餅 $ B $ の上に乗せて鏡餅を $ 1 $ つ作ることができます。 同時にいくつの鏡餅を作ることができるか求めてください。 より厳密には、以下ができるような最大の非負整数 $ K $ を求めてください。 - $ N $ 個の餅から $ 2K $ 個の餅を選んで $ K $ 個の $ 2 $ つ組に分け、それぞれの組について一方をもう一方の上に乗せることで鏡餅を $ K $ 個作る。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ A _ 1 $ $ A _ 2 $ $ \dotsc $ $ A _ N $

同時に $ K $ 個鏡餅を作れるような最大の $ K $ を出力せよ。

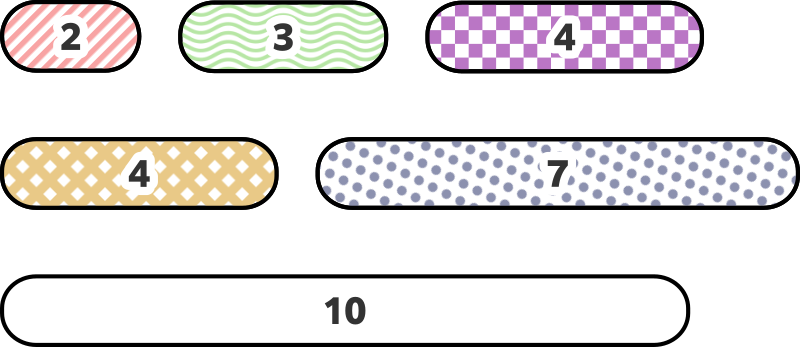
### Sample Explanation 1 与えられた餅の大きさは以下のようになっています。  このとき、以下の $ 3 $ つの鏡餅を同時に作ることができます。  $ 6 $ つの餅から $ 4 $ つ以上の鏡餅を作ることはできないので、`3` を出力してください。 ### Sample Explanation 2 鏡餅を $ 1 $ つも作ることができない場合もあります。 ### Constraints - $ 2\leq N\leq 5\times 10 ^ 5 $ - $ 1\leq A _ i\leq 10 ^ 9\ (1\leq i\leq N) $ - $ A _ i\leq A _ {i+1}\ (1\leq i\lt N) $ - 入力はすべて整数