AT_abc388_e [ABC388E] Simultaneous Kagamimochi

有 $N$ 个大小不一的饼。第 $i$ 个饼的大小为 $a_i$（$1 \le i \le N$）。 对于任意两个大小分别为 $a$ 和 $b$ 的饼 $A$ 和 $B$，如果 $a$ 小于或等于 $b$ 的一半，即 $a\le \frac{b}{2}$，则可以将饼 $A$ 放在饼 $B$ 上制作一个“镜饼”。 从 $N$ 个饼中任选两个，使得其中一个饼放在另一个饼上制作一个“镜饼”。 需要求出可以**同时**制作多少种不同的“镜饼”。 **Translate by [chinazhanghaoxun](https://luogu.com.cn/user/684848)。**

输入将以以下格式通过标准输入给出： > $N \ A_1\ A_2\ \dots\ A_N$

输出可以制作的镜饼数。 ### 数据限制 - $2\le N\le 5\times 10^5$ - $1\le A_i \le 10^9(1\le i\le N)$ - $A_i\le A_{i+1}(1\le i\le N)$ - 输入值均为整数

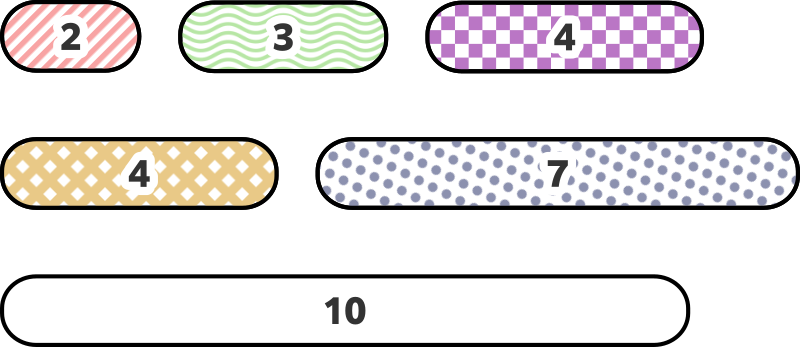
### Sample Explanation 1 与えられた餅の大きさは以下のようになっています。  このとき、以下の $ 3 $ つの鏡餅を同時に作ることができます。  $ 6 $ つの餅から $ 4 $ つ以上の鏡餅を作ることはできないので、`3` を出力してください。 ### Sample Explanation 2 鏡餅を $ 1 $ つも作ることができない場合もあります。 ### Constraints - $ 2\leq N\leq 5\times 10 ^ 5 $ - $ 1\leq A _ i\leq 10 ^ 9\ (1\leq i\leq N) $ - $ A _ i\leq A _ {i+1}\ (1\leq i\lt N) $ - 入力はすべて整数