AT_abc391_d [ABC391D] Gravity

There is a grid with $ 10^9 $ rows and $ W $ columns. The cell at the $ x $ -th column from the left and the $ y $ -th row from the **bottom** is denoted by $ (x,y) $ . There are $ N $ blocks. Each block is a $ 1 \times 1 $ square, and block $ i $ -th ( $ 1 \leq i \leq N $ ) is located at cell $ (X_i,Y_i) $ at time $ 0 $ . At times $ t=1,2,\dots,10^{100} $ , the blocks are moved according to the following rules: - If the entire bottom row is filled with blocks, then all blocks in the bottom row are removed. - For each remaining block, in order from bottom to top, perform the following: - If the block is in the bottom row, or if there is a block in the cell immediately below it, do nothing. - Otherwise, move the block one cell downward. You are given $ Q $ queries. For the $ j $ -th query ( $ 1 \leq j \leq Q $ ), answer whether block $ A_j $ exists at time $ T_j+0.5 $ .

The input is given from Standard Input in the following format: > $ N $ $ W $ $ X_1 $ $ Y_1 $ $ X_2 $ $ Y_2 $ $ \vdots $ $ X_N $ $ Y_N $ $ Q $ $ T_1 $ $ A_1 $ $ T_2 $ $ A_2 $ $ \vdots $ $ T_Q $ $ A_Q $

Print $ Q $ lines. The $ i $ -th line should contain `Yes` if block $ A_i $ exists at time $ T_i+0.5 $ , and `No` otherwise.

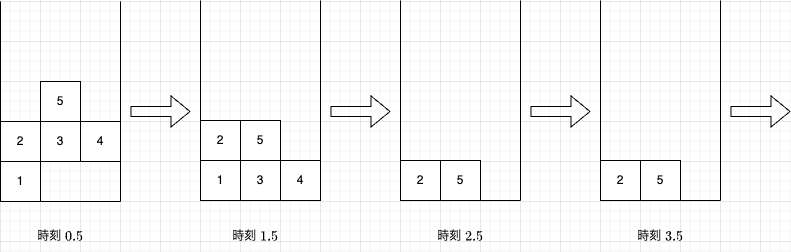
### Sample Explanation 1 The positions of the blocks change as follows: ("時刻" means "time.")  - Query $ 1 $ : At time $ 1.5 $ , block $ 1 $ exists, so the answer is `Yes`. - Query $ 2 $ : At time $ 1.5 $ , block $ 2 $ exists, so the answer is `Yes`. - Query $ 3 $ : Block $ 3 $ disappears at time $ 2 $ , so it does not exist at time $ 2.5 $ , and the answer is `No`. ### Constraints - $ 1 \leq N \leq 2 \times 10^5 $ - $ 1 \leq W \leq N $ - $ 1 \leq X_i \leq W $ - $ 1 \leq Y_i \leq 10^9 $ - $ (X_i,Y_i) \neq (X_j,Y_j) $ if $ i \neq j $ . - $ 1 \leq Q \leq 2 \times 10^5 $ - $ 1 \leq T_j \leq 10^9 $ - $ 1 \leq A_j \leq N $ - All input values are integers.