AT_abc391_d [ABC391D] Gravity

$ 10^9 $ 行 $ W $ 列のグリッドがあります。左から $ x $ 列目、**下から** $ y $ 行目のマスを $ (x,y) $ と表します。 $ N $ 個のブロックがあります。各ブロックは $ 1 \times 1 $ の正方形で、ブロック $ i $ $ (1 \leq i \leq N) $ は時刻 $ 0 $ にマス $ (X_i,Y_i) $ にあります。 時刻 $ t=1,2,\dots,10^{100} $ に、以下のルールに従ってブロックを動かします。 - グリッドの下から $ 1 $ 行目がすべてブロックで埋まっているならば、下から $ 1 $ 行目にあるブロックをすべて消滅させる。 - 残っているブロックについて、下にあるブロックから順番に、以下の操作を行う。 - ブロックが一番下の行にある、またはそのブロックの $ 1 $ つ下のマスにもブロックがあるならば、何もしない - そうでなければ、ブロックを $ 1 $ つ下のマスに動かす。 $ Q $ 個の質問が与えられます。 $ j $ 番目 $ (1 \leq j \leq Q) $ の質問では、時刻 $ T_j+0.5 $ にブロック $ A_j $ が存在するかどうか答えてください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ W $ $ X_1 $ $ Y_1 $ $ X_2 $ $ Y_2 $ $ \vdots $ $ X_N $ $ Y_N $ $ Q $ $ T_1 $ $ A_1 $ $ T_2 $ $ A_2 $ $ \vdots $ $ T_Q $ $ A_Q $

$ Q $ 行出力せよ。 $ i $ 行目には、時刻 $ T_i+0.5 $ にブロック $ A_i $ が存在するならば `Yes` を、存在しないならば `No` を出力せよ。

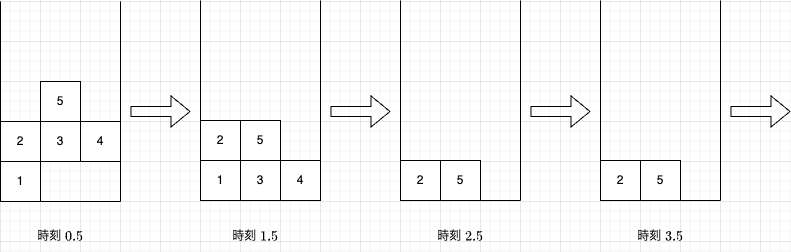
### Sample Explanation 1 ブロックの位置は以下のように変化します。  - 質問 $ 1 $ : 時刻 $ 1.5 $ にブロック $ 1 $ は存在するので、答えは `Yes` です。 - 質問 $ 2 $ : 時刻 $ 1.5 $ にブロック $ 2 $ は存在するので、答えは `Yes` です。 - 質問 $ 3 $ : ブロック $ 3 $ は時刻 $ 2 $ に消滅します。よって、時刻 $ 2.5 $ にブロック $ 3 $ は存在しないので、答えは `No` です。 ### Constraints - $ 1 \leq N \leq 2 \times 10^5 $ - $ 1 \leq W \leq N $ - $ 1 \leq X_i \leq W $ - $ 1 \leq Y_i \leq 10^9 $ - $ i \neq j $ なら $ (X_i,Y_i) \neq (X_j,Y_j) $ - $ 1 \leq Q \leq 2 \times 10^5 $ - $ 1 \leq T_j \leq 10^9 $ - $ 1 \leq A_j \leq N $ - 入力はすべて整数