AT_abc391_d [ABC391D] Gravity

[problemUrl]: https://atcoder.jp/contests/abc391/tasks/abc391_d 存在一个 $10^9$ 行 $W$ 列的网格。将左数第 $x$ 列、**下数**第 $y$ 行的单元格记为 $(x,y)$。 有 $N$ 个方块。每个方块是 $1 \times 1$ 的正方形，方块 $i$（$1 \leq i \leq N$）在时刻 $0$ 时位于单元格 $(X_i,Y_i)$。 在时刻 $t=1,2,\dots,10^{100}$ 时，按照以下规则移动方块： 1. 若网格下数第 $1$ 行所有列均被方块填满，则消除下数第 $1$ 行的所有方块。 2. 对于剩余的方块，从下往上的顺序依次进行以下操作： - 若方块位于最底行，或其下方相邻单元格已有方块，则不进行任何操作。 - 否则，将方块移动到下方相邻单元格。 给定 $Q$ 个询问。对于第 $j$ 个询问（$1 \leq j \leq Q$），请判断在时刻 $T_j+0.5$ 时方块 $A_j$ 是否存在。

输入通过标准输入按以下格式给出： > $N$ $W$ > $X_1$ $Y_1$ > $X_2$ $Y_2$ > $\vdots$ > $X_N$ $Y_N$ > $Q$ > $T_1$ $A_1$ > $T_2$ $A_2$ > $\vdots$ > $T_Q$ $A_Q$

输出 $Q$ 行。第 $i$ 行输出 `Yes`（若时刻 $T_i+0.5$ 时方块 $A_i$ 存在）或 `No`（若不存在）。

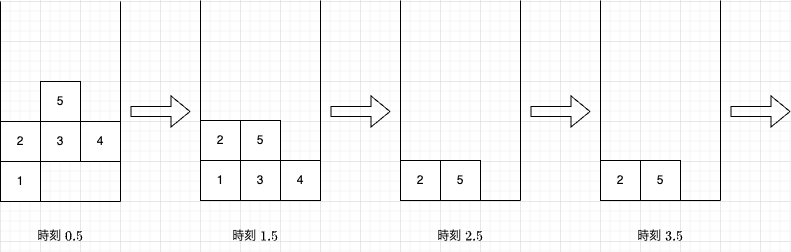
### 约束条件 - $1 \leq N \leq 2 \times 10^5$ - $1 \leq W \leq N$ - $1 \leq X_i \leq W$ - $1 \leq Y_i \leq 10^9$ - $i \neq j$ 时 $(X_i,Y_i) \neq (X_j,Y_j)$ - $1 \leq Q \leq 2 \times 10^5$ - $1 \leq T_j \leq 10^9$ - $1 \leq A_j \leq N$ - 输入均为整数 ### 样例解释 1 方块位置变化如下图所示：  - 询问 $1$：时刻 $1.5$ 时方块 $1$ 存在，输出 `Yes`。 - 询问 $2$：时刻 $1.5$ 时方块 $2$ 存在，输出 `Yes`。 - 询问 $3$：方块 $3$ 在时刻 $2$ 被消除，因此时刻 $2.5$ 时不存在，输出 `No`。 翻译由 DeepSeek R1 完成