AT_abc392_e [ABC392E] Cables and Servers

There are $ N $ servers numbered from $ 1 $ to $ N $ and $ M $ cables numbered from $ 1 $ to $ M $ . Cable $ i $ connects servers $ A_i $ and $ B_i $ bidirectionally. By performing the following operation some number of times (possibly zero), make all servers connected via cables. - Operation: Choose one cable and reconnect one of its ends to a different server. Find the minimum number of operations required and output an operation sequence achieving this minimum.

The input is given from Standard Input in the following format: > $ N $ $ M $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_M $ $ B_M $

Let the minimum number of operations be $ K $ . Print $ K+1 $ lines. - The first line should contain $ K $ . - The $ (i+1) $ -th line should contain three space-separated integers: the number of the cable chosen in the $ i $ -th operation, the server number that was originally connected at that end, and the server number to which it is connected after the operation, in this order. If there are multiple valid solutions, any one of them will be accepted.

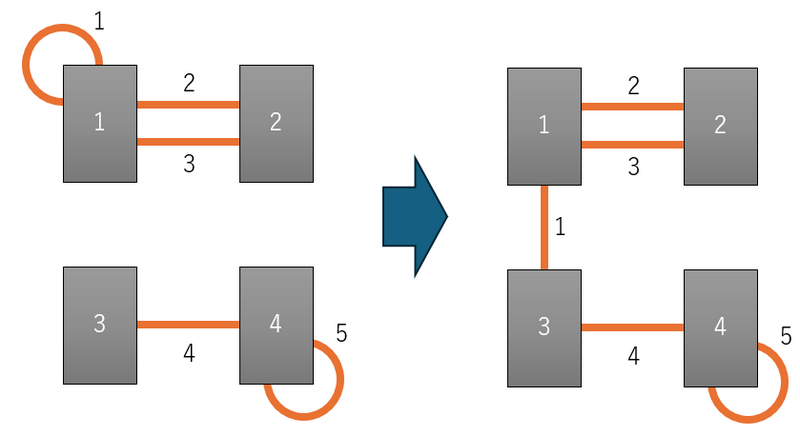
### Sample Explanation 1 By reconnecting the end of cable $ 1 $ that is connected to server $ 1 $ to server $ 3 $ , the servers can be connected via cables.  Operations such as reconnecting the end of cable $ 5 $ that is connected to server $ 4 $ to server $ 1 $ , or reconnecting the end of cable $ 2 $ that is connected to server $ 2 $ to server $ 3 $ , will also result in all servers being connected and are considered correct. ### Sample Explanation 2 No operation may be necessary. ### Constraints - $ 2 \leq N \leq 2\times 10^5 $ - $ N-1 \leq M \leq 2\times 10^5 $ - $ 1 \leq A_i, B_i \leq N $ - All input values are integers.