AT_abc392_e [ABC392E] Cables and Servers

$ 1 $ から $ N $ の番号がついた $ N $ 台のサーバーと $ 1 $ から $ M $ の番号がついた $ M $ 本のケーブルがあります。 ケーブル $ i $ はサーバー $ A_i $ とサーバー $ B_i $ を双方向に結んでいます。 以下の操作を何回か( $ 0 $ 回でもよい)行うことで、全てのサーバー同士がケーブルを介して繋がっているようにしてください。 - 操作：ケーブルを $ 1 $ つ選び、その片方の端を別のサーバーに繋ぎ変える 操作の最小回数と、最小回数となる操作列を求めてください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_M $ $ B_M $

操作回数の最小値を $ K $ とする。 $ K+1 $ 行出力せよ。 $ 1 $ 行目には $ K $ を出力せよ。 $ i+1 $ 行目には $ i $ 回目の操作で選ぶケーブルの番号、繋ぎ変える前に繋がっていたサーバーの番号、繋ぎ変えたあと繋がっているサーバーの番号をこの順に空白区切りで出力せよ。 条件を満たす解が複数存在する場合、どれを出力しても正解とみなされる。

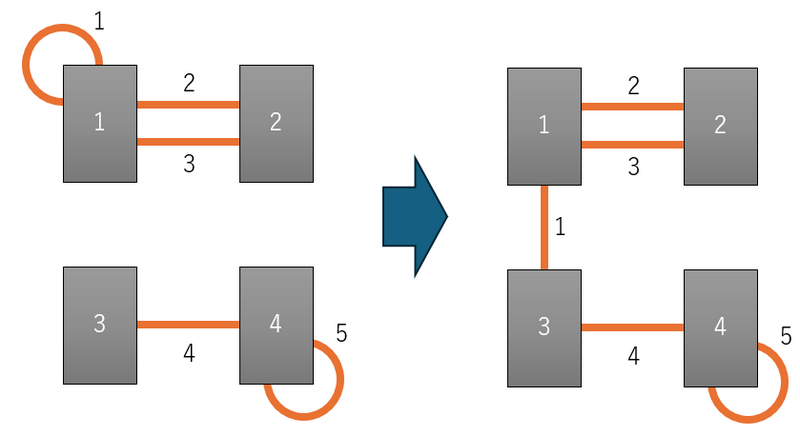
### Sample Explanation 1 ケーブル $ 1 $ のサーバー $ 1 $ に繋がっている側の端をサーバー $ 3 $ に繋ぎ変えることで、サーバー同士がケーブルを介して繋がっている状態にすることができます。  このほか、「ケーブル $ 5 $ のサーバー $ 4 $ に繋がっている側の端をサーバー $ 1 $ に繋ぎ変える」という操作や、「ケーブル $ 2 $ のサーバー $ 2 $ に繋がっている側の端をサーバー $ 3 $ に繋ぎ変える」という操作でもサーバー同士がケーブルを介して繋がっている状態にすることができるため、正解とみなされます。 ### Sample Explanation 2 操作をする必要がないこともあります。 ### Constraints - $ 2 \leq N \leq 2\times 10^5 $ - $ N-1 \leq M \leq 2\times 10^5 $ - $ 1 \leq A_i,B_i \leq N $ - 入力は全て整数である