AT_abc395_d [ABC395D] Pigeon Swap

There are $ N $ pigeons labeled $ 1, 2, \ldots, N $ and $ N $ nests labeled $ 1, 2, \ldots, N $ . Initially, pigeon $ i $ $ (1 \leq i \leq N) $ is in nest $ i $ . You will perform $ Q $ operations on these pigeons. There are three types of operations: - Type $ 1 $ : You are given integers $ a $ and $ b $ $ (1 \leq a \leq N, 1 \leq b \leq N) $ . Take pigeon $ a $ out of its current nest and move it to nest $ b $ . - Type $ 2 $ : You are given integers $ a $ and $ b $ $ (1 \leq a < b \leq N) $ . Move all pigeons in nest $ a $ to nest $ b $ , and move all pigeons in nest $ b $ to nest $ a $ . These two moves happen simultaneously. - Type $ 3 $ : You are given an integer $ a $ $ (1 \leq a \leq N) $ . Pigeon $ a $ reports the label of the nest it is currently in. Print the result of each Type $ 3 $ operation in the order the operations are given.

The input is given from Standard Input in the following format: > $ N $ $ Q $ $ op _ 1 $ $ op _ 2 $ $ \vdots $ $ op _ Q $ Here, $ op _ i $ on the line $ i+1 $ represents the $ i $ -th operation in one of the following formats. If the $ i $ -th operation is of Type $ 1 $ , $ op _ i $ is in the following format: > $ 1 $ $ a $ $ b $ This corresponds to a Type $ 1 $ operation with the given integers being $ a $ and $ b $ . If the $ i $ -th operation is of Type $ 2 $ , $ op _ i $ is in the following format: > $ 2 $ $ a $ $ b $ This corresponds to a Type $ 2 $ operation with the given integers being $ a $ and $ b $ . If the $ i $ -th operation is of Type $ 3 $ , $ op _ i $ is in the following format: > $ 3 $ $ a $ This corresponds to a Type $ 3 $ operation with the given integer being $ a $ .

Let the number of Type $ 3 $ operations be $ q $ . Print $ q $ lines. The $ i $ -th line $ (1 \leq i \leq q) $ should contain the nest number reported in the $ i $ -th Type $ 3 $ operation.

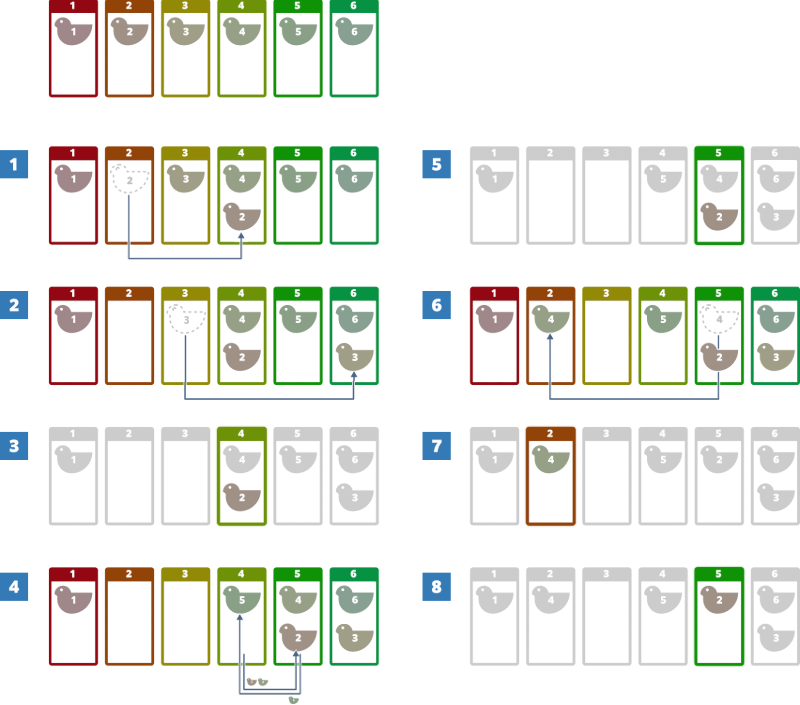
### Sample Explanation 1 In the operations given, the pigeons move as shown in the figure below:  The nest numbers to be reported for the Type $ 3 $ operations are $ 4,5,2,5 $ . Print `4`, `5`, `2`, `5` on separate lines. ### Sample Explanation 2 The destination nest of a Type $ 1 $ operation may be the same as the nest the pigeon is currently in. ### Constraints - $ 1 \leq N \leq 10^6 $ - $ 1 \leq Q \leq 3 \times 10^5 $ - Every operation is of Type $ 1 $ , $ 2 $ , or $ 3 $ . - All operations are valid according to the problem statement. - There is at least one Type $ 3 $ operation. - All input values are integers.