AT_abc395_e [ABC395E] Flip Edge

You are given a directed graph with $ N $ vertices and $ M $ edges. The $ i $ -th edge $ (1 \leq i \leq M) $ is a directed edge from vertex $ u _ i $ to vertex $ v _ i $ . Initially, you are at vertex $ 1 $ . You want to repeat the following operations until you reach vertex $ N $ : - Perform one of the two operations below: - Move along a directed edge from your current vertex. This incurs a cost of $ 1 $ . More precisely, if you are at vertex $ v $ , choose a vertex $ u $ such that there is a directed edge from $ v $ to $ u $ , and move to vertex $ u $ . - Reverse the direction of all edges. This incurs a cost of $ X $ . More precisely, if and only if there was a directed edge from $ v $ to $ u $ immediately before this operation, there is a directed edge from $ u $ to $ v $ immediately after this operation. It is guaranteed that, for the given graph, you can reach vertex $ N $ from vertex $ 1 $ by repeating these operations. Find the minimum total cost required to reach vertex $ N $ .

The input is given from Standard Input in the following format: > $ N $ $ M $ $ X $ $ u _ 1 $ $ v _ 1 $ $ u _ 2 $ $ v _ 2 $ $ \vdots $ $ u _ M $ $ v _ M $

Print the minimum total cost required to reach vertex $ N $ .

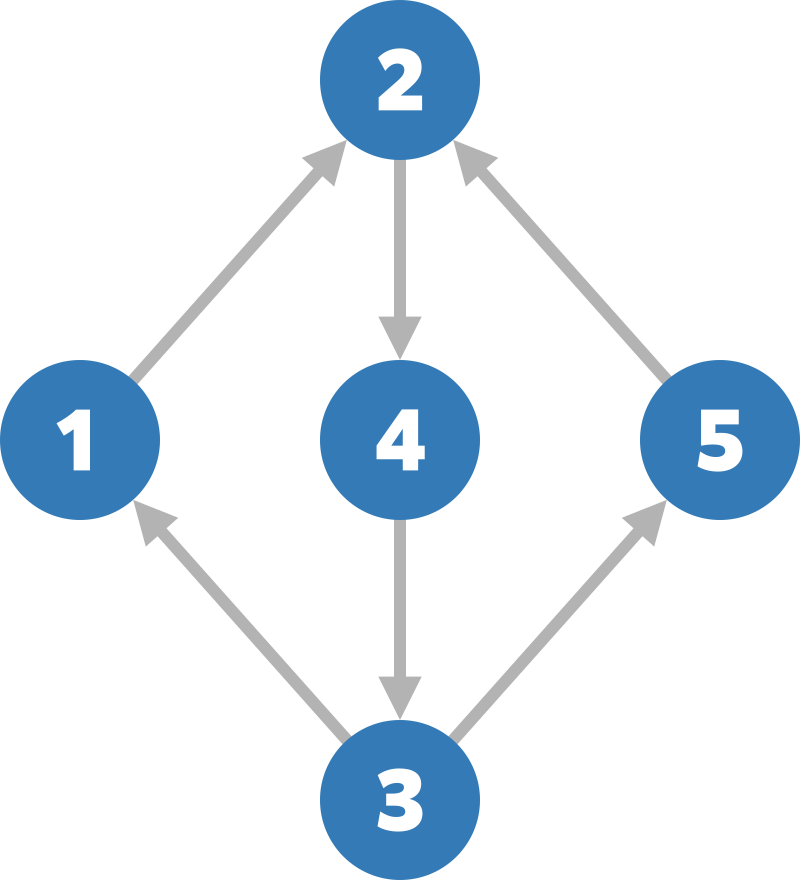
### Sample Explanation 1 The given graph looks like this:  You can reach vertex $ 5 $ with a total cost of $ 4 $ by doing the following: - Move to vertex $ 2 $ at a cost of $ 1 $ . - Move to vertex $ 4 $ at a cost of $ 1 $ . - Move to vertex $ 3 $ at a cost of $ 1 $ . - Move to vertex $ 5 $ at a cost of $ 1 $ . It is impossible to reach vertex $ 5 $ with a total cost of $ 3 $ or less, so print `4`. ### Sample Explanation 2 The graph is the same as in Sample 1, but the cost to reverse edges is different. You can reach vertex 5 with a total cost of $ 3 $ as follows: - Move to vertex $ 2 $ at a cost of $ 1 $ . - Reverse all edges at a cost of $ 1 $ . - Move to vertex $ 5 $ at a cost of $ 1 $ . It is impossible to reach vertex $ 5 $ with a total cost of $ 2 $ or less, so print `3`. ### Sample Explanation 3 Note that the answer may exceed the $ 32 $ -bit integer range. ### Constraints - $ 2 \leq N \leq 2 \times 10^5 $ - $ 1 \leq M \leq 2 \times 10^5 $ - $ 1 \leq X \leq 10^9 $ - $ 1 \leq u _ i \leq N \ (1 \leq i \leq M) $ - $ 1 \leq v _ i \leq N \ (1 \leq i \leq M) $ - For the given graph, it is guaranteed that you can reach vertex $ N $ from vertex $ 1 $ by the operations described. - All input values are integers.