AT_abc395_e [ABC395E] Flip Edge

$ N $ 頂点 $ M $ 辺の有向グラフが与えられます。 $ i $ 番目 $ (1\leq i\leq M) $ の辺は頂点 $ u _ i $ から頂点 $ v _ i $ への有向辺です。 はじめ、あなたは頂点 $ 1 $ におり、以下の操作を繰り返して頂点 $ N $ にたどり着きたいです。 - 次の操作のうちのいずれかを行う。 - 今いる頂点から辺をたどって移動する。コストが $ 1 $ かかる。より厳密には、今いる頂点を $ v $ として、 $ v $ から $ u $ への有向辺が存在するような $ u $ を $ 1 $ つ選び、頂点 $ u $ へ移動する。 - すべての辺の向きを反転する。コストが $ X $ かかる。より厳密には、この操作の直前に $ v $ から $ u $ への有向辺が存在しているとき、かつそのときに限り、この操作の直後に $ u $ から $ v $ への有向辺が存在する。 与えられるグラフにおいて、上の操作を繰り返して頂点 $ 1 $ から頂点 $ N $ にたどり着くことができることが保証されます。 頂点 $ N $ にたどりつくまでにかかるコストの総和の最小値を求めてください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ X $ $ u _ 1 $ $ v _ 1 $ $ u _ 2 $ $ v _ 2 $ $ \vdots $ $ u _ M $ $ v _ M $

頂点 $ N $ にたどりつくまでにかかるコストの総和の最小値を出力せよ。

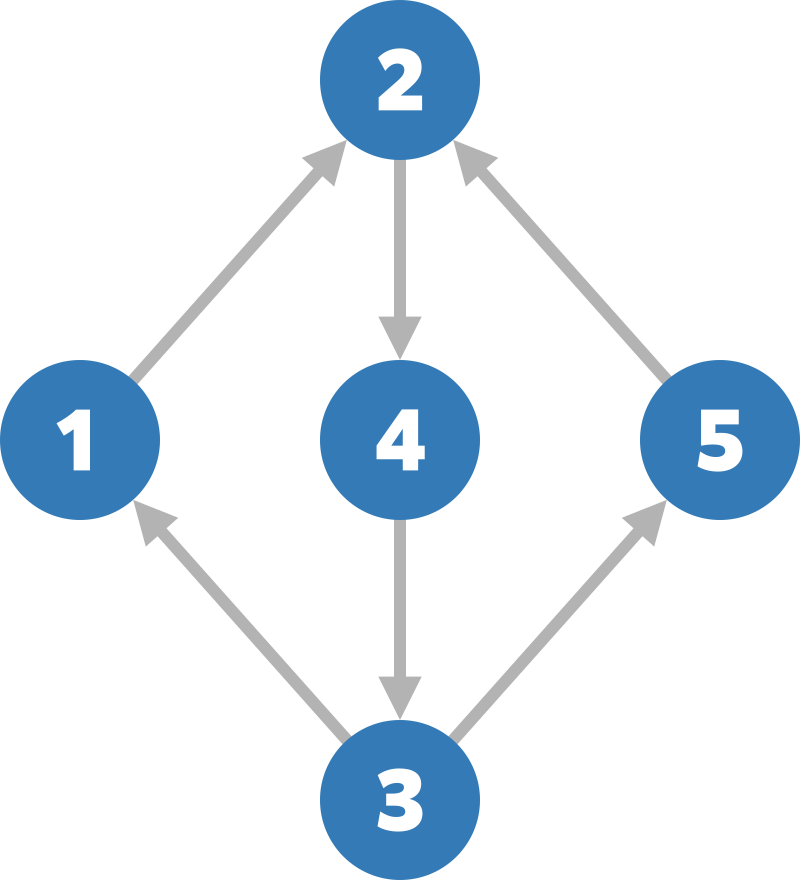
### Sample Explanation 1 与えられたグラフは以下のようになります。  次のように操作を行うことで、コストの総和を $ 4 $ として頂点 $ 5 $ にたどり着くことができます。 - コストを $ 1 $ かけて頂点 $ 2 $ に移動する。 - コストを $ 1 $ かけて頂点 $ 4 $ に移動する。 - コストを $ 1 $ かけて頂点 $ 3 $ に移動する。 - コストを $ 1 $ かけて頂点 $ 5 $ に移動する。 コストの総和を $ 3 $ 以下として頂点 $ 5 $ にたどり着くことはできないため、`4` を出力してください。 ### Sample Explanation 2 与えられたグラフは入出力例 1 と同じですが、辺を反転させるのにかかるコストが異なります。 次のように操作を行うことで、コストの総和を $ 3 $ として頂点 $ 5 $ にたどり着くことができます。 - コストを $ 1 $ かけて頂点 $ 2 $ に移動する。 - コストを $ 1 $ かけてすべての辺を反転させる。 - コストを $ 1 $ かけて頂点 $ 5 $ に移動する。 コストの総和を $ 2 $ 以下として頂点 $ 5 $ にたどり着くことはできないため、`3` を出力してください。 ### Sample Explanation 3 答えが $ 32\operatorname{bit} $ 整数に収まらない場合があることに注意してください。 ### Constraints - $ 2\leq N\leq2\times10 ^ 5 $ - $ 1\leq M\leq2\times10 ^ 5 $ - $ 1\leq X\leq10 ^ 9 $ - $ 1\leq u _ i\leq N\ (1\leq i\leq M) $ - $ 1\leq v _ i\leq N\ (1\leq i\leq M) $ - 与えられるグラフにおいて、上記の操作を繰り返して頂点 $ 1 $ から頂点 $ N $ にたどり着くことができる。 - 入力はすべて整数