AT_abc396_g [ABC396G] Flip Row or Col

给定一个 $H$ 行 $W$ 列的网格，每个格子中写有 $0$ 或 $1$。从上往下第 $i$ 行、从左往右第 $j$ 列的格子中写有整数 $A_{i,j}$。 你可以对网格进行以下两种操作任意次，顺序不限： - 操作 X：选择一个整数 $x$ $(1 \leq x \leq H)$。对于所有 $1 \leq y \leq W$，将 $A_{x,y}$ 替换为 $1 - A_{x,y}$。 - 操作 Y：选择一个整数 $y$ $(1 \leq y \leq W)$。对于所有 $1 \leq x \leq H$，将 $A_{x,y}$ 替换为 $1 - A_{x,y}$。 请计算操作结束后，$\displaystyle \sum_{x=1}^H \sum_{y=1}^W A_{x,y}$ 可能达到的最小值。

输入通过标准输入给出，格式如下： > $H$ $W$ > $A_{1,1}A_{1,2}\ldots A_{1,W}$ > $A_{2,1}A_{2,2}\ldots A_{2,W}$ > $\vdots$ > $A_{H,1}A_{H,2}\ldots A_{H,W}$

输出答案。

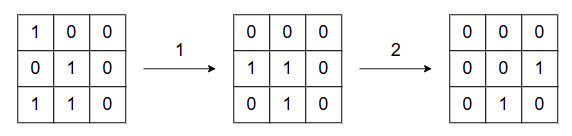
### 约束条件 - $1 \leq H \leq 2 \times 10^5$ - $1 \leq W \leq 18$ - $H$ 和 $W$ 为整数 - $A_{i,1}A_{i,2}\ldots A_{i,W}$ 是由 `0` 和 `1` 组成的长度为 $W$ 的字符串 ### 样例解释 1 通过以下操作，可以使网格状态变化如下  ，此时 $\displaystyle \sum_{x=1}^H \sum_{y=1}^W A_{x,y} = 2$： 1. 执行操作 Y，选择 $y=1$ 2. 执行操作 X，选择 $x=2$ 由于无法使 $\displaystyle \sum_{x=1}^H \sum_{y=1}^W A_{x,y} \leq 1$，因此答案为 $2$。 翻译由 DeepSeek R1 完成