AT_abc396_g [ABC396G] Flip Row or Col

There is a $ H \times W $ grid, and each cell contains $ 0 $ or $ 1 $ . The cell at the $ i $ -th row from the top and the $ j $ -th column from the left contains an integer $ A_{i,j} $ . You can perform the following two operations any number of times in any order: - Operation X: Choose an integer $ x $ ( $ 1 \leq x \leq H $ ). For every integer $ 1 \leq y \leq W $ , replace $ A_{x,y} $ with $ 1 - A_{x,y} $ . - Operation Y: Choose an integer $ y $ ( $ 1 \leq y \leq W $ ). For every integer $ 1 \leq x \leq H $ , replace $ A_{x,y} $ with $ 1 - A_{x,y} $ . Find the minimum possible value of $ \displaystyle \sum_{x=1}^H\sum_{y=1}^W A_{x,y} $ after the process.

The input is given from Standard Input in the following format: > $ H $ $ W $ $ A_{1,1}A_{1,2}\ldots A_{1,W} $ $ A_{2,1}A_{2,2}\ldots A_{2,W} $ $ \vdots $ $ A_{H,1}A_{H,2}\ldots A_{H,W} $

Print the answer.

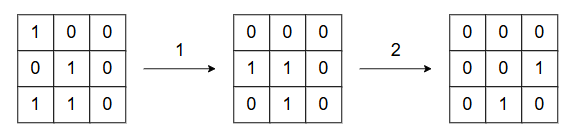
### Sample Explanation 1 By performing the following operations, the grid changes as shown below, and you get $ \displaystyle \sum_{x=1}^H\sum_{y=1}^W A_{x,y} = 2 $ . 1. Operation Y with $ y=1 $ 2. Operation X with $ x=2 $  It is impossible to make $ \displaystyle \sum_{x=1}^H\sum_{y=1}^W A_{x,y} \leq 1 $ , so the answer is $ 2 $ . ### Constraints - $ 1 \leq H \leq 2\times 10^5 $ - $ 1 \leq W \leq 18 $ - $ H $ and $ W $ are integers. - $ A_{i,1}A_{i,2}\ldots A_{i,W} $ is a length- $ W $ string consisting of `0` and `1`.