AT_abc398_d [ABC398D] Bonfire

There is an infinitely large two-dimensional grid, with a campfire at coordinate $ (0,0) $ . At time $ t=0 $ , smoke exists only at cell $ (0,0) $ . You are given a length- $ N $ string $ S $ consisting of `N`, `W`, `S`, `E`. At times $ t=1,2,\dots,N $ , the following happen in order: - Wind blows, and all the smoke present at that time moves as follows: - If the $ t $ -th character of $ S $ is `N`, smoke in cell $ (r,c) $ moves to cell $ (r-1,c) $ . - If it is `W`, smoke in cell $ (r,c) $ moves to cell $ (r,c-1) $ . - If it is `S`, smoke in cell $ (r,c) $ moves to cell $ (r+1,c) $ . - If it is `E`, smoke in cell $ (r,c) $ moves to cell $ (r,c+1) $ . - If there is no smoke in cell $ (0,0) $ , new smoke is generated at cell $ (0,0) $ . Takahashi is standing at cell $ (R,C) $ . For each integer $ 1 \le t \le N $ , determine if smoke exists at cell $ (R,C) $ at time $ t+0.5 $ , and print the response according to the required format.

The input is given from Standard Input in the following format: > $ N $ $ R $ $ C $ $ S $

Print an $ N $ -character string consisting of `0` and `1`. The $ t $ -th character ( $ 1 \le t \le N $ ) should be: - `1` if smoke exists at cell $ (R,C) $ at time $ t+0.5 $ , and - `0` otherwise.

### Sample Explanation 1 At times $ 1.5,2.5,4.5,6.5 $ , there is no smoke at cell $ (-2,1) $ . At times $ 3.5,5.5 $ , there is smoke at cell $ (-2,1) $ . Hence, output `001010`. In the figures below, taking cell $ (0,0) $ with the campfire as a reference, cell $ (r,c) $ is drawn: - $ -r $ cells up if $ r < 0 $ , - $ r $ cells down if $ r \ge 0 $ , - $ -c $ cells left if $ c < 0 $ , - $ c $ cells right if $ c \ge 0 $ . 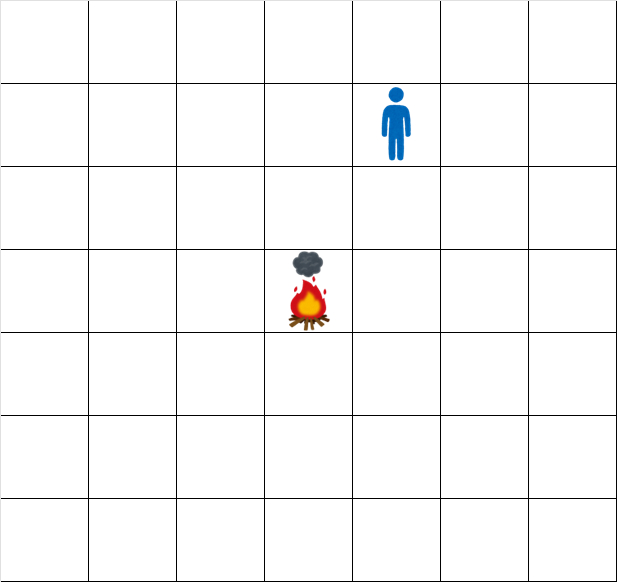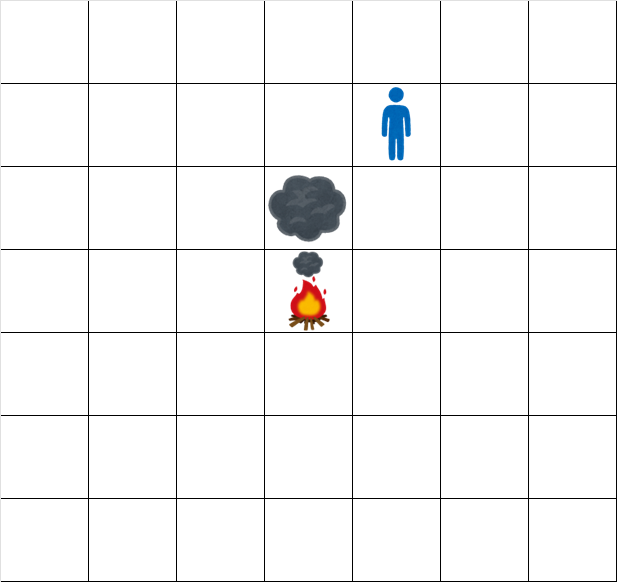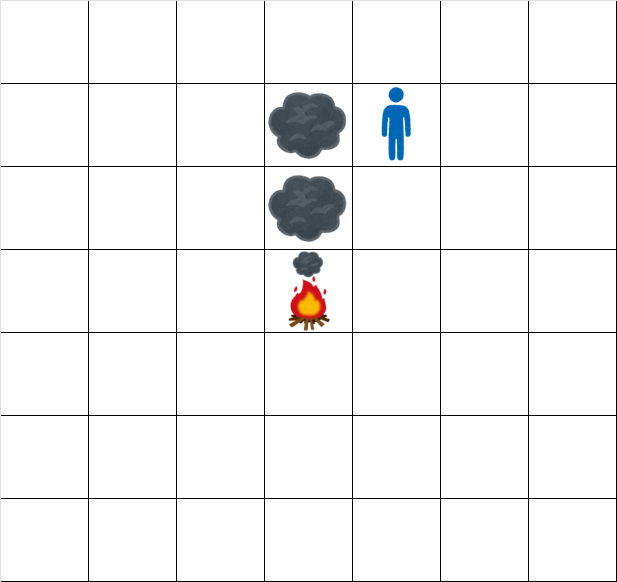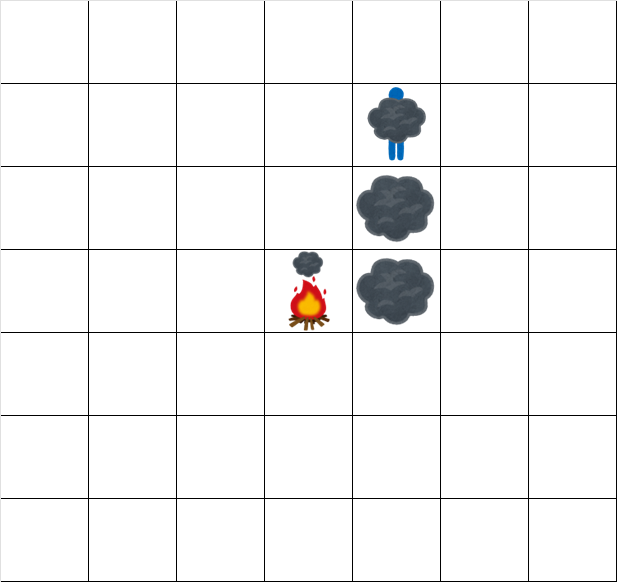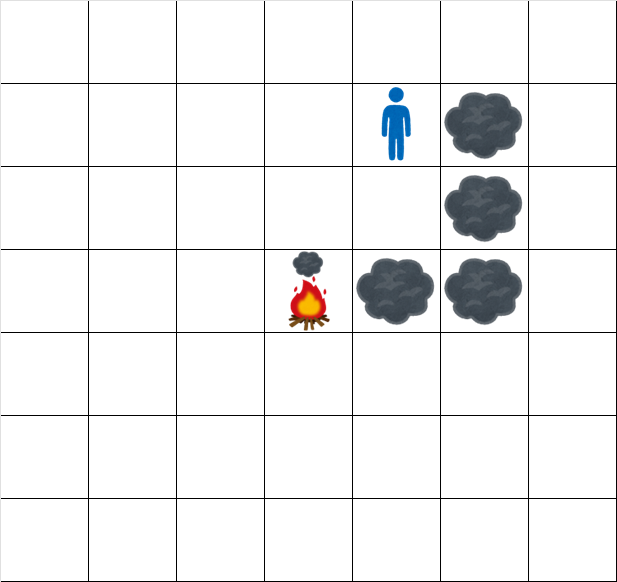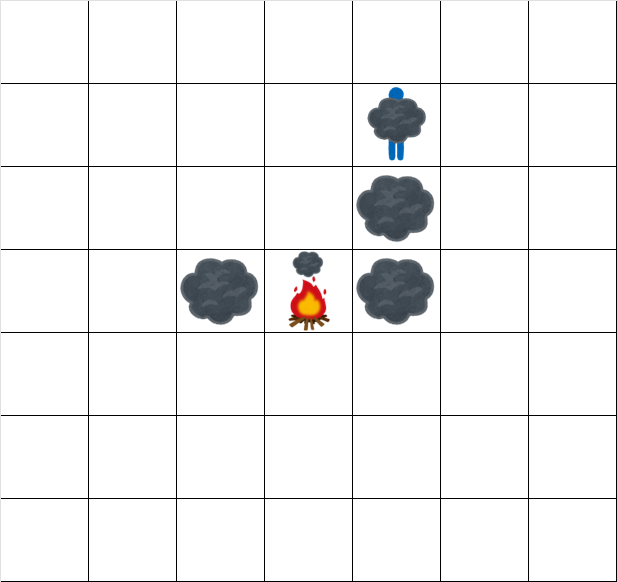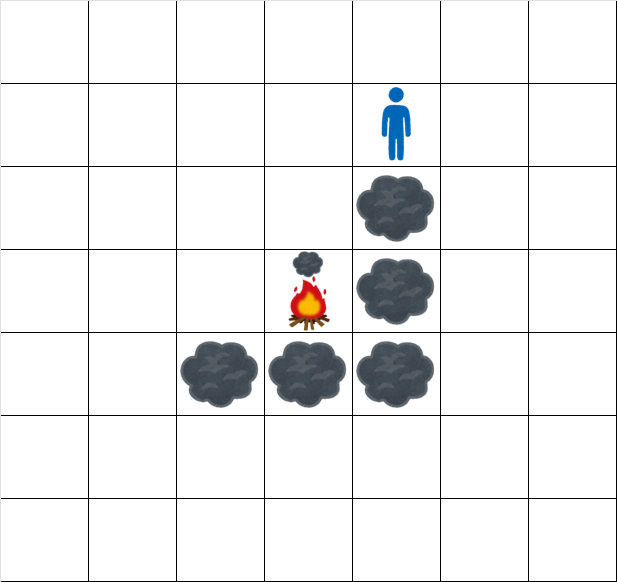The grid at time $ 0.5 $ looks like:  The grid at time $ 1.5 $ looks like:  The grid at time $ 2.5 $ looks like:  The grid at time $ 3.5 $ looks like:  The grid at time $ 4.5 $ looks like:  The grid at time $ 5.5 $ looks like:  The grid at time $ 6.5 $ looks like:  ### Constraints - $ N $ is an integer between $ 1 $ and $ 200000 $ , inclusive. - $ S $ is a length $ N $ string consisting of `N`, `W`, `S`, `E`. - $ R $ and $ C $ are integers between $ -N $ and $ N $ , inclusive. - $ (R,C) \neq (0,0) $