AT_abc398_d [ABC398D] Bonfire

無限に広い $ 2 $ 次元グリッドがあり、このグリッドの座標 $ (0,0) $ に焚き火があります。 時刻 $ t=0 $ では、マス $ (0,0) $ にのみ煙が存在します。 `N`, `W`, `S`, `E` からなる長さ $ N $ の文字列 $ S $ が与えられ、時刻 $ t=1,2,\dots,N $ では次の現象が順番に発生します。 - 風が吹き、現時点で存在する全ての煙が以下の通りに移動する。 - $ S $ の $ t $ 文字目が `N` であるとき、マス $ (r,c) $ にある煙がマス $ (r-1,c) $ に移動する。 - $ S $ の $ t $ 文字目が `W` であるとき、マス $ (r,c) $ にある煙がマス $ (r,c-1) $ に移動する。 - $ S $ の $ t $ 文字目が `S` であるとき、マス $ (r,c) $ にある煙がマス $ (r+1,c) $ に移動する。 - $ S $ の $ t $ 文字目が `E` であるとき、マス $ (r,c) $ にある煙がマス $ (r,c+1) $ に移動する。 - マス $ (0,0) $ に煙が存在しない場合、新たな煙がマス $ (0,0) $ に生成される。 高橋君はマス $ (R,C) $ に立っています。 整数 $ 1 \le t \le N $ について、時刻 $ t+0.5 $ においてマス $ (R,C) $ に煙が存在するか判定し、出力欄の形式に従って出力してください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ R $ $ C $ $ S $

答えを $ N $ 文字の `0`, `1` からなる文字列として出力せよ。 出力する文字列のうち $ t $ 文字目 ( $ 1 \le t \le N $ ) は次の通りにせよ。 - 時刻 $ t+0.5 $ においてマス $ (R,C) $ に煙が存在するなら `1` - 時刻 $ t+0.5 $ においてマス $ (R,C) $ に煙が存在しないなら `0`

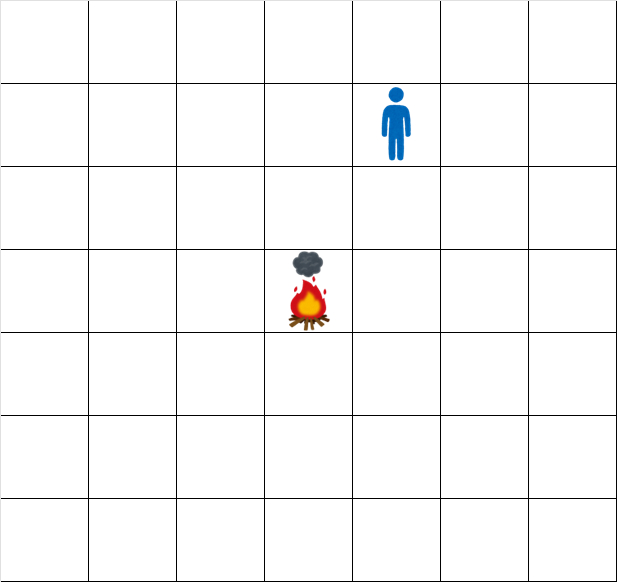
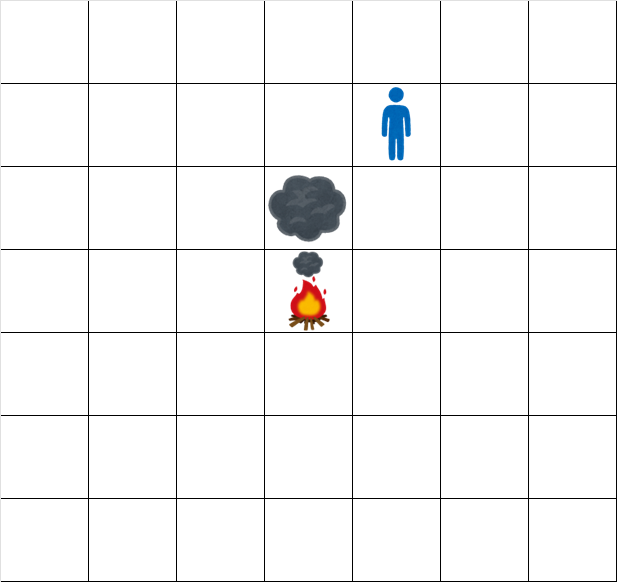
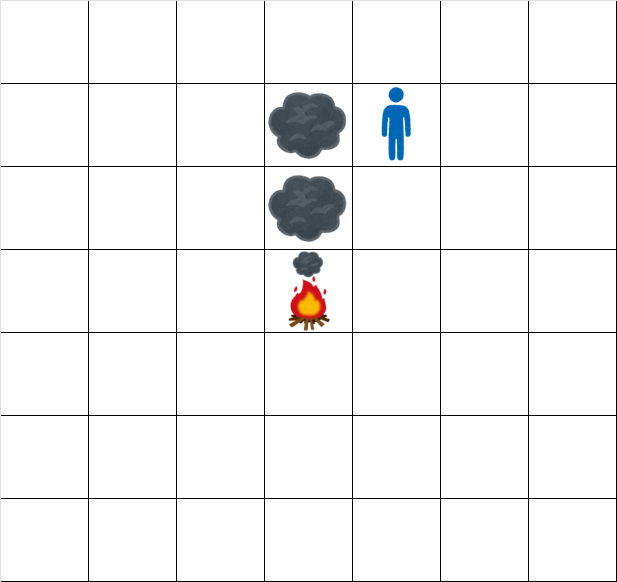
### Sample Explanation 1 時刻 $ 1.5,2.5,4.5,6.5 $ ではマス $ (-2,1) $ には煙が存在せず、時刻 $ 3.5,5.5 $ ではマス $ (-2,1) $ に煙が存在します。 よって、 `001010` と出力します。 図では焚き火のあるマス $ (0,0) $ を基準として、マス $ (r,c) $ を - $ r < 0 $ なら $ -r $ マス上に - $ r \ge 0 $ なら $ r $ マス下に - $ c < 0 $ なら $ -c $ マス左に - $ c \ge 0 $ なら $ c $ マス右に 描画します。 時刻 $ 0.5 $ でのグリッドの状態は次の通りです。  時刻 $ 1.5 $ でのグリッドの状態は次の通りです。  時刻 $ 2.5 $ でのグリッドの状態は次の通りです。  時刻 $ 3.5 $ でのグリッドの状態は次の通りです。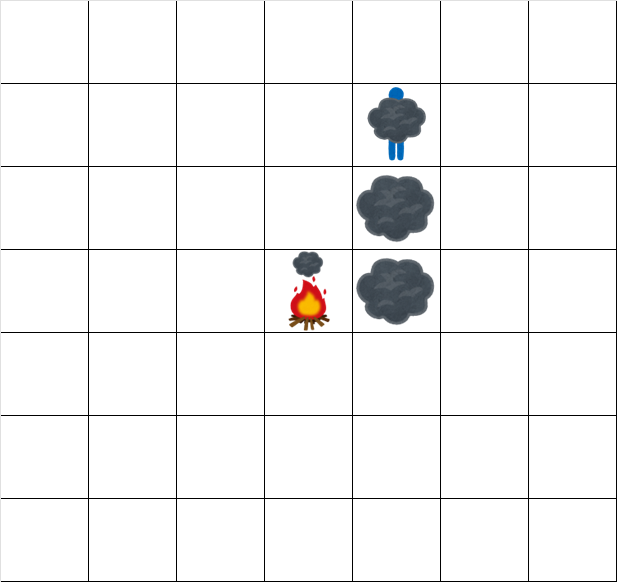  時刻 $ 4.5 $ でのグリッドの状態は次の通りです。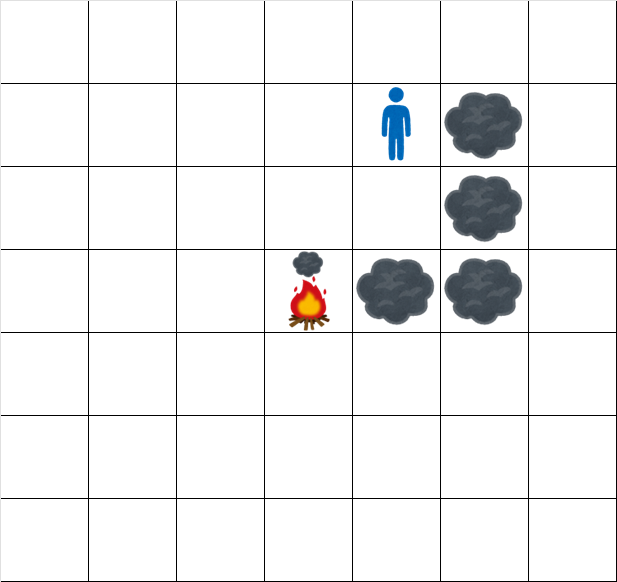  時刻 $ 5.5 $ でのグリッドの状態は次の通りです。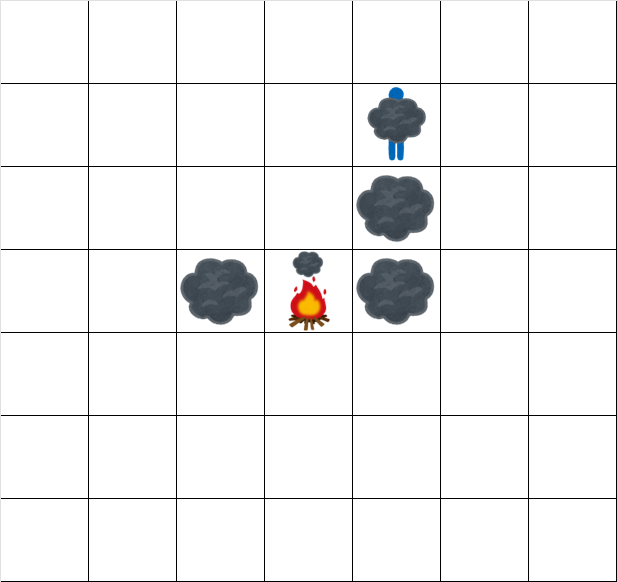  時刻 $ 6.5 $ でのグリッドの状態は次の通りです。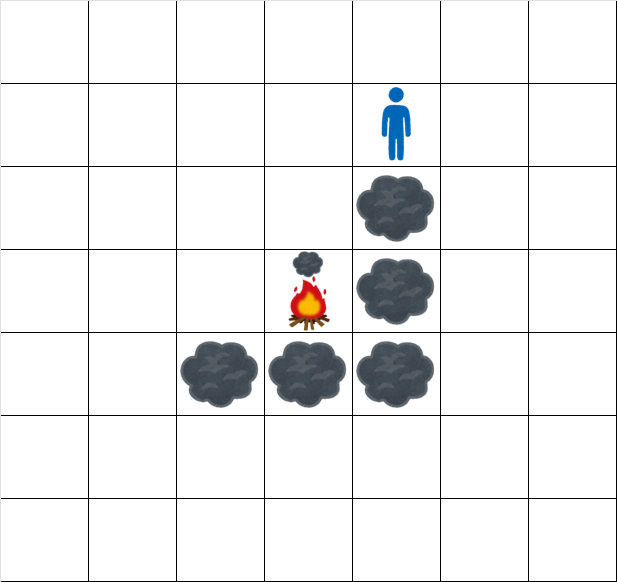  ### Constraints - $ N $ は $ 1 $ 以上 $ 200000 $ 以下の整数 - $ S $ は `N`, `W`, `S`, `E` からなる長さ $ N $ の文字列 - $ R,C $ は $ -N $ 以上 $ N $ 以下の整数 - $ (R,C) \neq (0,0) $