AT_abc398_d [ABC398D] Bonfire

[problemUrl]: https://atcoder.jp/contests/abc398/tasks/abc398_d 在无限广阔的二维网格中，坐标 $(0, 0)$ 处有一堆篝火。 在时刻 $t=0$ 时，仅单元格 $(0, 0)$ 存在烟雾。 给定一个由 `N`、`W`、`S`、`E` 组成且长度为 $N$ 的字符串 $S$，在时刻 $t=1,2,\dots,N$ 时，将按顺序发生以下现象： - 风吹过时，当前存在的所有烟雾将按以下规则移动： - 若 $S$ 的第 $t$ 个字符为 `N`，则单元格 $(r, c)$ 的烟雾移动到 $(r-1, c)$。 - 若 $S$ 的第 $t$ 个字符为 `W`，则单元格 $(r, c)$ 的烟雾移动到 $(r, c-1)$。 - 若 $S$ 的第 $t$ 个字符为 `S`，则单元格 $(r, c)$ 的烟雾移动到 $(r+1, c)$。 - 若 $S$ 的第 $t$ 个字符为 `E`，则单元格 $(r, c)$ 的烟雾移动到 $(r, c+1)$。 - 若此时单元格 $(0, 0)$ 没有烟雾，则在该位置生成新的烟雾。 高桥君位于坐标 $(R, C)$ 处。 对于每个整数 $1 \leq t \leq N$，请判断在时刻 $t+0.5$ 时单元格 $(R, C)$ 是否存在烟雾，并按输出格式要求输出结果。

输入通过标准输入给出，格式如下： > $N$ $R$ $C$ > $S$

将答案作为由 $N$ 个 `0` 和 `1` 组成的字符串输出。 输出字符串的第 $t$ 个字符 ($1 \leq t \leq N$) 应满足以下规则： - 若时刻 $t+0.5$ 时单元格 $(R, C)$ 存在烟雾，则为 `1` - 若时刻 $t+0.5$ 时单元格 $(R, C)$ 不存在烟雾，则为 `0`

### 约束条件 - $N$ 是 $1$ 以上 $200000$ 以下的整数 - $S$ 是由 `N`、`W`、`S`、`E` 组成且长度为 $N$ 的字符串 - $R, C$ 是 $-N$ 以上 $N$ 以下的整数 - $(R, C) \neq (0, 0)$ ### 样例解释 1 在时刻 $1.5$、$2.5$、$4.5$、$6.5$ 时，单元格 $(-2, 1)$ 不存在烟雾；在时刻 $3.5$、$5.5$ 时存在烟雾。因此输出 `001010`。 图示中以篝火所在的单元格 $(0, 0)$ 为基准： - 若 $r < 0$，则单元格 $(r, c)$ 位于上方 $|r|$ 格 - 若 $r \geq 0$，则单元格 $(r, c)$ 位于下方 $r$ 格 - 若 $c < 0$，则单元格 $(r, c)$ 位于左侧 $|c|$ 格 - 若 $c \geq 0$，则单元格 $(r, c)$ 位于右侧 $c$ 格 各时刻的网格状态如下（以下为原题图片链接，此处保留描述）： - 时刻 $0.5$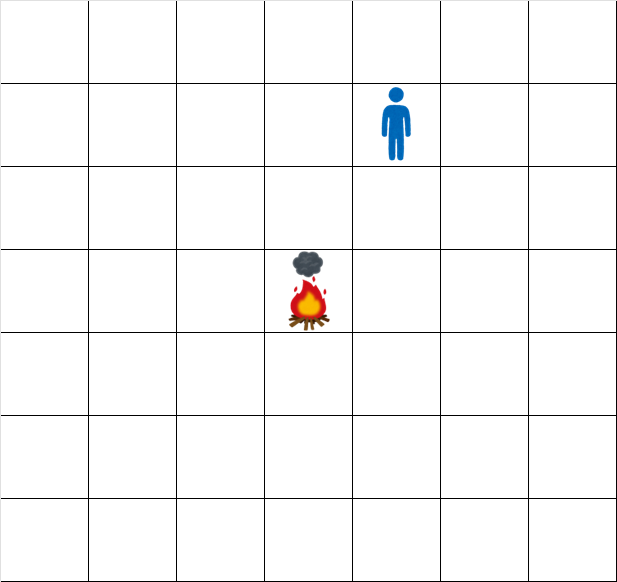： - 时刻 $1.5$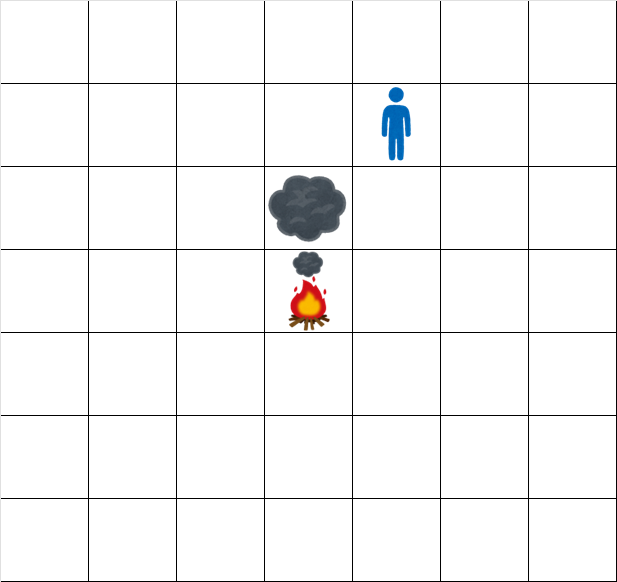： - 时刻 $2.5$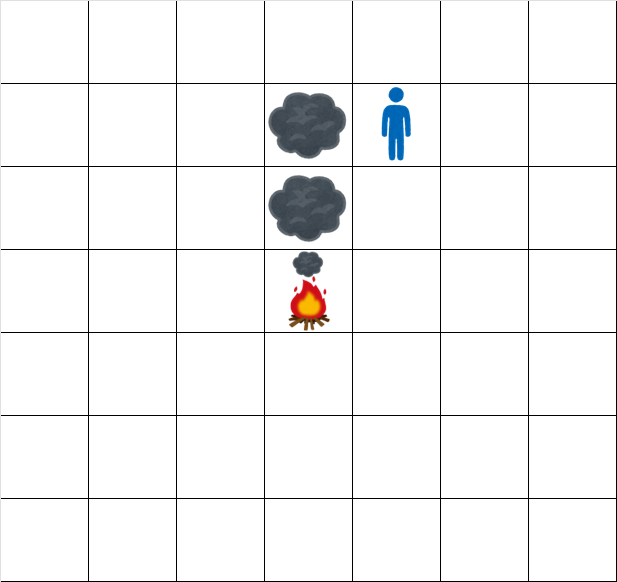： - 时刻 $3.5$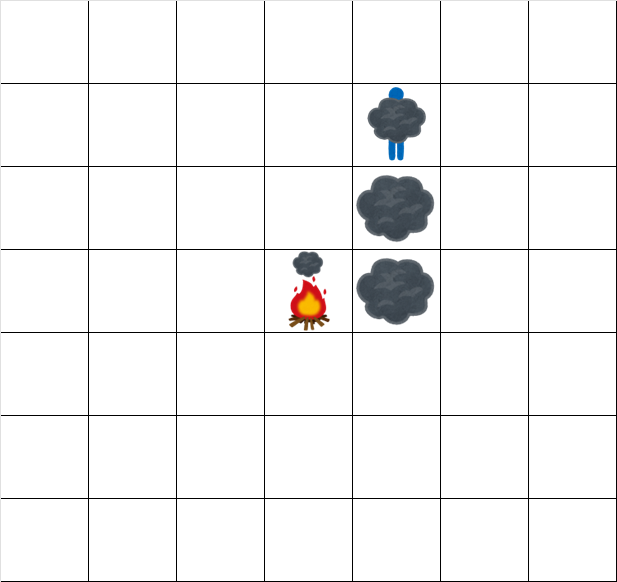： - 时刻 $4.5$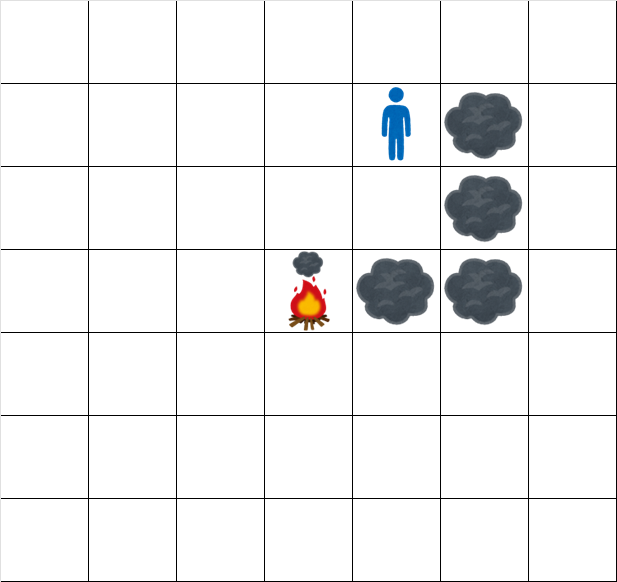： - 时刻 $5.5$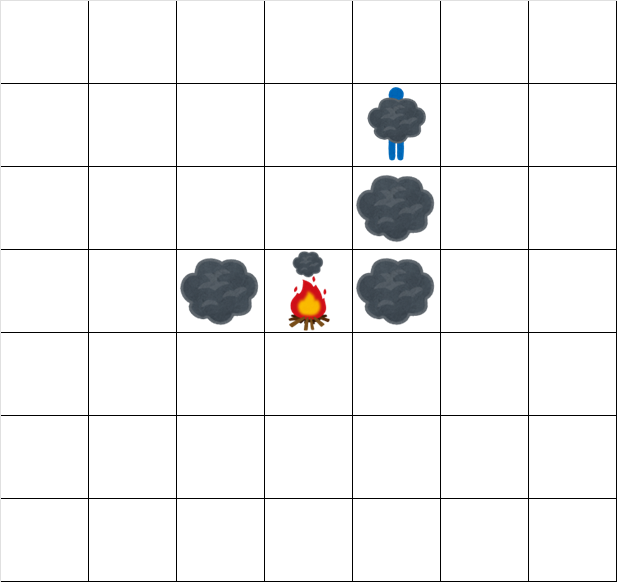： - 时刻 $6.5$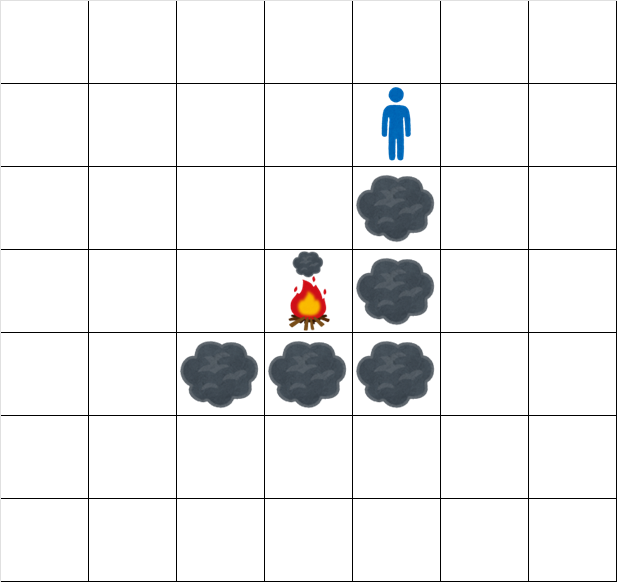： 翻译由 DeepSeek R1 完成