AT_abc401_g [ABC401G] Push Simultaneously

There are $ N $ people and $ N $ buttons on a plane. The plane has an origin, and the coordinates $ (x, y) $ represents the position that is $ x $ meters east and $ y $ meters north of the origin. The $ i $ ‑th person $ (1 \le i \le N) $ starts at $ (\mathit{sx}_i,\mathit{sy}_i) $ . The $ i $ ‑th button $ (1 \le i \le N) $ is located at $ (\mathit{gx}_i,\mathit{gy}_i) $ . The people want to move and press these $ N $ buttons **simultaneously**. A button can be pressed only by a person who is at the same coordinate as that button. The time required to press a button after reaching its coordinate is $ 0 $ seconds. Each person can move in any direction with speed at most $ 1 $ meter per second. More formally, if the position of the $ i $ ‑th person $ t $ seconds after the start is $ (x_i(t), y_i(t)) $ , all of the following must hold: - $ x_i(0) = \mathit{sx}_i $ ; - $ y_i(0) = \mathit{sy}_i $ ; - For all non‑negative real numbers $ t_0, t_1 $ , the distance between $ (x_i(t_0), y_i(t_0)) $ and $ (x_i(t_1), y_i(t_1)) $ is at most $ |t_0 - t_1| $ . Find the time required for the people to achieve the goal. Formally, find the minimum $ t $ that satisfies the following condition: - It is possible to set $ x_i $ and $ y_i $ under the above conditions so that, for every integer $ j\ (1\leq j\leq N) $ and every real number $ t ^ \prime\ (t ^ \prime\gt t) $ , there exists an integer $ i\ (1\leq i\leq N) $ with $ (x _ i(t ^ \prime),y _ i(t ^ \prime))=(\mathit{gx} _ j,\mathit{gy} _ j) $ .

The input is given from Standard Input in the following format: > $ N $ $ \mathit{sx}_1 $ $ \mathit{sy}_1 $ $ \mathit{sx}_2 $ $ \mathit{sy}_2 $ $ \vdots $ $ \mathit{sx}_N $ $ \mathit{sy}_N $ $ \mathit{gx}_1 $ $ \mathit{gy}_1 $ $ \mathit{gx}_2 $ $ \mathit{gy}_2 $ $ \vdots $ $ \mathit{gx}_N $ $ \mathit{gy}_N $

Print the time required for the $ N $ people to press the $ N $ buttons simultaneously. Your output is considered correct if the relative error from the true value is at most $ 10^{-6} $ .

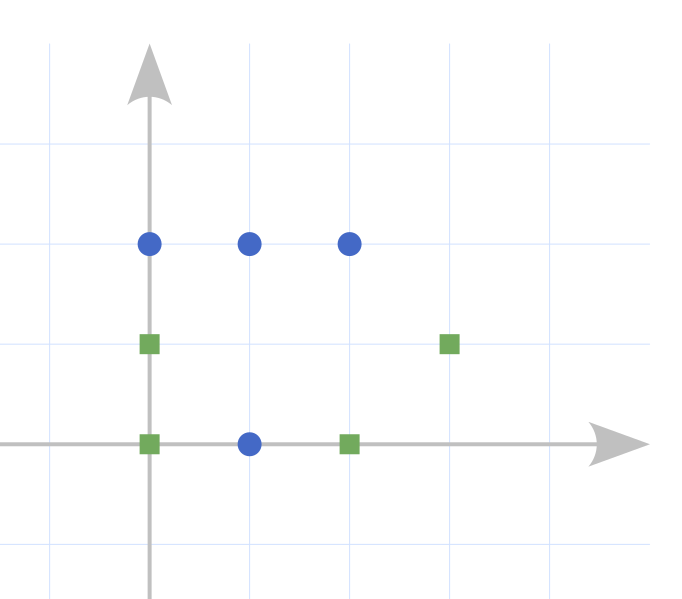
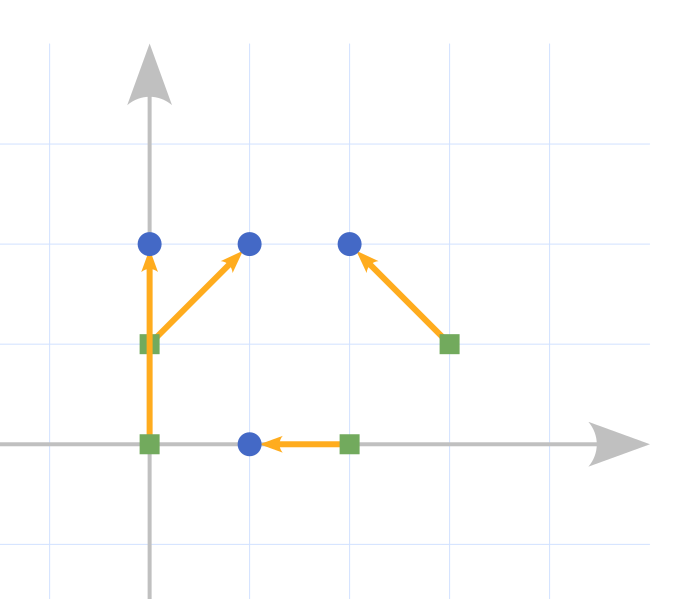
### Sample Explanation 1 Initially, the positions of the people and buttons are as shown below.  Suppose persons $ 1,2,3,4 $ move straight toward buttons $ 1,3,2,4 $ , respectively.  They reach their respective buttons after $ 2 $ , $ \sqrt2 $ , $ 1 $ , and $ \sqrt2 $ seconds. Thus, all buttons can be pressed simultaneously $ 2 $ seconds after the start. Conversely, they cannot press all buttons simultaneously earlier than $ 2 $ seconds, so print `2`. Because an output is accepted if its relative error from the true value is at most $ 10^{-6} $ , outputs such as `1.999998` or `2.00000014` are also considered correct for this test case. ### Sample Explanation 2 Note that the input coordinates may not fit in $ 32 $ ‑bit integers. ### Constraints - $ 1\leq N\leq 300 $ - $ 0\leq\mathit{sx} _ i\leq10 ^ {18}\ (1\leq i\leq N) $ - $ 0\leq\mathit{sy} _ i\leq10 ^ {18}\ (1\leq i\leq N) $ - $ 0\leq\mathit{gx} _ i\leq10 ^ {18}\ (1\leq i\leq N) $ - $ 0\leq\mathit{gy} _ i\leq10 ^ {18}\ (1\leq i\leq N) $ - $ (\mathit{sx} _ i,\mathit{sy} _ i)\neq(\mathit{sx} _ j,\mathit{sy} _ j)\ (1\leq i\lt j\leq N) $ - $ (\mathit{gx} _ i,\mathit{gy} _ i)\neq(\mathit{gx} _ j,\mathit{gy} _ j)\ (1\leq i\lt j\leq N) $ - $ (\mathit{sx} _ i,\mathit{sy} _ i)\neq(\mathit{gx} _ j,\mathit{gy} _ j)\ (1\leq i\leq N,1\leq j\leq N) $ - All input values are integers.