AT_abc401_g [ABC401G] Push Simultaneously

平面上に $ N $ 人の高橋くんと $ N $ 個のボタンがあります。 平面上には原点があり、原点から東に $ x $ メートル進み、北に $ y $ メートル進んだ位置を座標 $ (x,y) $ で表すこととします。 $ i $ 番目 $ (1\leq i\leq N) $ の高橋くんははじめ座標 $ (\mathit{sx} _ i,\mathit{sy} _ i) $ にいます。 $ i $ 番目 $ (1\leq i\leq N) $ のボタンは座標 $ (\mathit{gx} _ i,\mathit{gy} _ i) $ にあります。 高橋くんたちはそれぞれ移動をした後、この $ N $ 個のボタンを**一斉に**押したいです。 各ボタンは、そのボタンがある座標にいる高橋くんだけが押すことができます。 ボタンが存在する座標に到達してからボタンを押すのに必要な時間は $ 0 $ 秒です。 それぞれの高橋くんは秒速 $ 1 $ メートル以下の速さで好きな方向に進むことができます。 より厳密には、 $ i $ 番目の高橋くんがスタートから $ t $ 秒後にいる座標を $ (x _ i(t),y _ i(t)) $ としたとき、次の条件がすべて成り立っている必要があります。 - $ x _ i(0)=\mathit{sx} _ i $ - $ y _ i(0)=\mathit{sy} _ i $ - すべての非負実数 $ t _ 0,t _ 1 $ について、点 $ (x _ i(t _ 0),y _ i(t _ 0)) $ と点 $ (x _ i(t _ 1),y _ i(t _ 1)) $ の距離は $ |t _ 0-t _ 1| $ 以下 高橋くんたちが目標を達成するために必要な時間を求めてください。 厳密には、次の条件を満たすことができる $ t $ の最小値を求めてください。 - $ x _ i,y _ i $ を上の条件を満たすように適切に定めたとき、すべての整数 $ j\ (1\leq j\leq N) $ および実数 $ t ^ \prime\ (t ^ \prime\gt t) $ に対して、ある整数 $ i\ (1\leq i\leq N) $ が存在して $ (x _ i(t ^ \prime),y _ i(t ^ \prime))=(\mathit{gx} _ j,\mathit{gy} _ j) $ が成り立つ。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ \mathit{sx} _ 1 $ $ \mathit{sy} _ 1 $ $ \mathit{sx} _ 2 $ $ \mathit{sy} _ 2 $ $ \vdots $ $ \mathit{sx} _ N $ $ \mathit{sy} _ N $ $ \mathit{gx} _ 1 $ $ \mathit{gy} _ 1 $ $ \mathit{gx} _ 2 $ $ \mathit{gy} _ 2 $ $ \vdots $ $ \mathit{gx} _ N $ $ \mathit{gy} _ N $

$ N $ 人の高橋くんが $ N $ 個のボタンを同時に押すのに必要な時間を出力せよ。 真の値と出力との相対誤差が $ 10 ^ {-6} $ 以下のとき、正解と判定される。

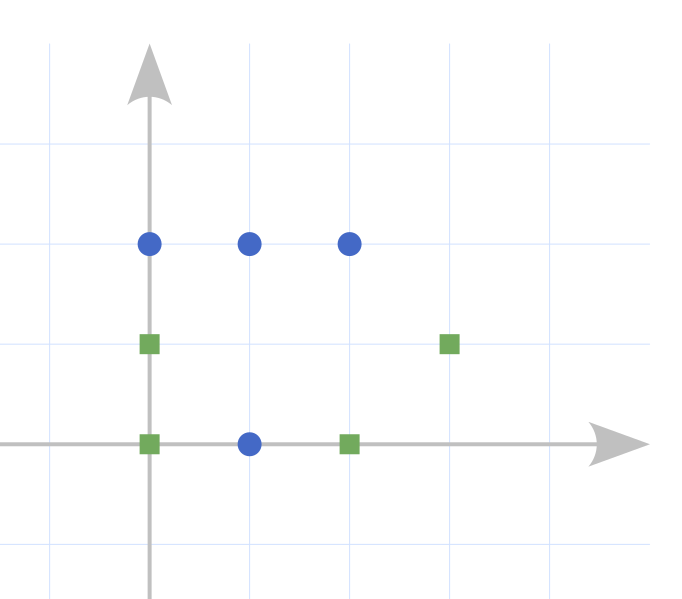
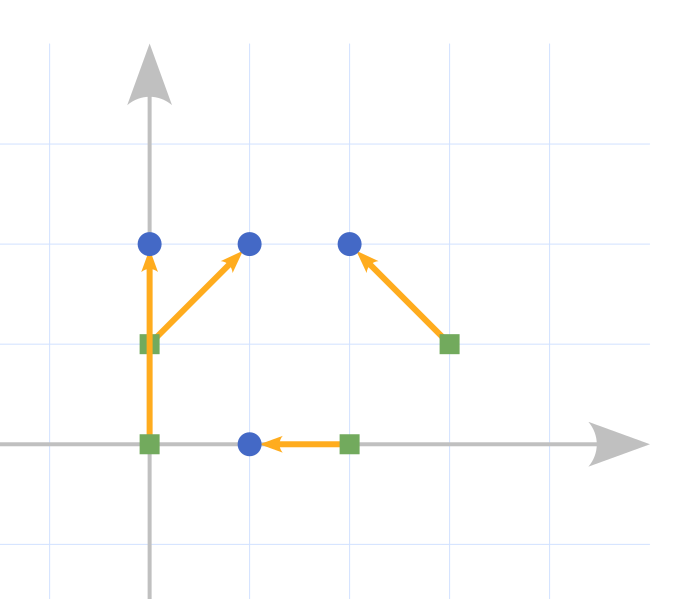
### Sample Explanation 1 はじめ、高橋くんとボタンの位置関係は以下のようになっています。  $ 1,2,3,4 $ 番目の高橋くんが、それぞれ $ 1,3,2,4 $ 番目のボタンに向かってまっすぐ動くことを考えます。  すると、高橋くんたちはそれぞれスタートから $ 2 $ 秒後、 $ \sqrt2 $ 秒後、 $ 1 $ 秒後、 $ \sqrt2 $ 秒後には対応するボタンがある座標に到着しています。 よって、スタートから $ 2 $ 秒後にすべてのボタンを一斉に押すことができます。 逆に、スタートから $ 2 $ 秒経つより前にすべてのボタンを一斉に押すことはできないので、`2` を出力してください。 答えの真の値と出力との相対誤差が $ 10 ^ {-6} $ 以下であれば正解と判定されるため、`1.999998` や `2.00000014` などを出力してもこのケースに対する正答と判定されます。 ### Sample Explanation 2 入力される座標が $ 32\operatorname{bit} $ 整数におさまらない場合があることに注意してください。 ### Constraints - $ 1\leq N\leq 300 $ - $ 0\leq\mathit{sx} _ i\leq10 ^ {18}\ (1\leq i\leq N) $ - $ 0\leq\mathit{sy} _ i\leq10 ^ {18}\ (1\leq i\leq N) $ - $ 0\leq\mathit{gx} _ i\leq10 ^ {18}\ (1\leq i\leq N) $ - $ 0\leq\mathit{gy} _ i\leq10 ^ {18}\ (1\leq i\leq N) $ - $ (\mathit{sx} _ i,\mathit{sy} _ i)\neq(\mathit{sx} _ j,\mathit{sy} _ j)\ (1\leq i\lt j\leq N) $ - $ (\mathit{gx} _ i,\mathit{gy} _ i)\neq(\mathit{gx} _ j,\mathit{gy} _ j)\ (1\leq i\lt j\leq N) $ - $ (\mathit{sx} _ i,\mathit{sy} _ i)\neq(\mathit{gx} _ j,\mathit{gy} _ j)\ (1\leq i\leq N,1\leq j\leq N) $ - 入力はすべて整数