AT_abc402_d [ABC402D] Line Crossing
题目描述
[problemUrl]: https://atcoder.jp/contests/abc402/tasks/abc402_d
在圆周上等间距地排列着 $N$ 个点,按顺时针方向依次编号为 $1,2,\ldots,N$。
有 $M$ 条互不相同的**直线**,其中第 $i$ 条直线通过两个不同的点:点 $A_i$ 和点 $B_i$($1 \leq i \leq M$)。
请计算满足以下两个条件的整数对 $(i,j)$ 的个数:
1. $1 \leq i < j \leq M$
2. 第 $i$ 条直线与第 $j$ 条直线相交
输入格式
输入通过标准输入给出,格式如下:
> $N$ $M$
> $A_1$ $B_1$
> $A_2$ $B_2$
> $\vdots$
> $A_M$ $B_M$
输出格式
输出答案。
说明/提示
### 约束条件
- $2 \leq N \leq 10^6$
- $1 \leq M \leq 3 \times 10^{5}$
- $1 \leq A_i < B_i \leq N$($1 \leq i \leq M$)
- $(A_i,B_i) \neq (A_j,B_j)$($i \neq j$)
- 输入中的所有数值均为整数
### 样例解释 1
如图所示,圆周上有 $8$ 个点和 $3$ 条直线:
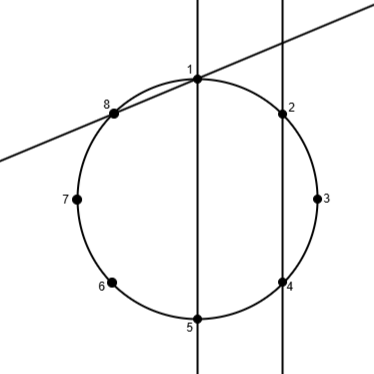
- 第 $1$ 条直线与第 $2$ 条直线相交
- 第 $1$ 条直线与第 $3$ 条直线不相交
- 第 $2$ 条直线与第 $3$ 条直线相交
满足条件的整数对为 $(i,j)=(1,2),(2,3)$,因此输出 $2$。
翻译由 DeepSeek V3 完成