AT_abc402_d [ABC402D] Line Crossing

There are $ N $ equally spaced points on a circle labeled clockwise as $ 1,2,\ldots,N $ . There are $ M $ distinct **lines**, where the $ i $ -th line passes through two distinct points $ A_i $ and $ B_i $ $ (1 \leq i \leq M) $ . Find the number of pairs $ (i,j) $ satisfying: - $ 1 \le i < j \le M $ , and - the $ i $ -th and $ j $ -th lines intersect.

The input is given from Standard Input in the following format: > $ N $ $ M $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_M $ $ B_M $

Print the answer.

### Sample Explanation 1 As shown in the diagram below, there are eight points and three lines on the circle. 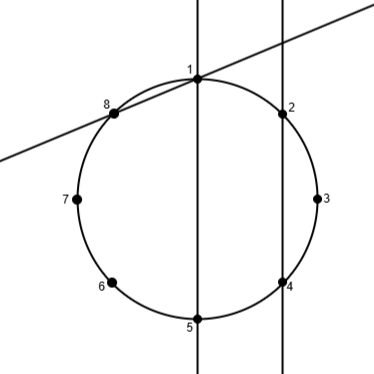 The 1st and 2nd lines intersect. The 1st and 3rd lines do not intersect. The 2nd and 3rd lines intersect. Since the pairs $ (i,j)=(1,2),(2,3) $ satisfy the conditions, print $ 2 $ . ### Constraints - $ 2 \leq N \leq 10^6 $ - $ 1 \leq M \leq 3 \times 10^{5} $ - $ 1 \leq A_i < B_i \leq N $ $ (1 \leq i \leq M) $ - $ (A_i,B_i) \neq (A_j,B_j) $ $ (i \neq j) $ - All input values are integers.