AT_abc402_d [ABC402D] Line Crossing
Description
円周上に $ N $ 個の点が等間隔に並んでおり、時計回りに $ 1,2,\ldots,N $ と番号がつけられています。
$ M $ 本の相異なる**直線**があり、 $ i $ 本目の直線は異なる $ 2 $ つの点、点 $ A_i $ と点 $ B_i $ を通る直線です。 $ (1 \leq i \leq M) $
以下の $ 2 $ つの条件をともに満たすような整数の組 $ (i,j) $ の個数を求めてください。
- $ 1 \leq i < j \leq M $
- $ i $ 本目の直線と $ j $ 本目の直線は交わる
Input Format
入力は以下の形式で標準入力から与えられる。
> $ N $ $ M $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_M $ $ B_M $
Output Format
答えを出力せよ。
Explanation/Hint
### Sample Explanation 1
次の図のように円周上に $ 8 $ 個の点と $ 3 $ 本の直線があります。 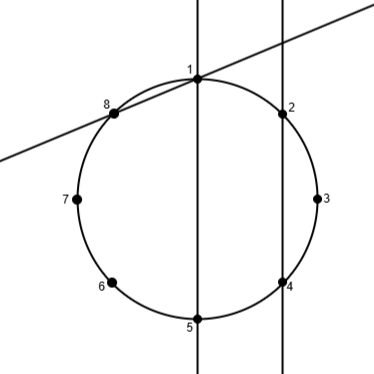
$ 1 $ 本目の直線と $ 2 $ 本目の直線は交わります。 $ 1 $ 本目の直線と $ 3 $ 本目の直線は交わりません。 $ 2 $ 本目の直線と $ 3 $ 本目の直線は交わります。 $ (i,j)=(1,2),(2,3) $ の $ 2 $ つの組が条件を満たすため、 $ 2 $ を出力します。
### Constraints
- $ 2 \leq N \leq 10^6 $
- $ 1 \leq M \leq 3 \times 10^{5} $
- $ 1 \leq A_i < B_i \leq N $ $ (1 \leq i \leq M) $
- $ (A_i,B_i) \neq (A_j,B_j) $ $ (i \neq j) $
- 入力は全て整数