AT_abc404_c [ABC404C] Cycle Graph?

You are given a simple undirected graph with $ N $ vertices and $ M $ edges. The vertices are numbered $ 1,2,\dots,N $ and the edges are numbered $ 1,2,\dots,M $ . Edge $ i $ connects vertices $ A_i $ and $ B_i $ . Determine whether this graph is a cycle graph. Definition of simple undirected graphA simple undirected graph is a graph with undirected edges without self-loops or multi-edges. Definition of cycle graphAn $ N $ -vertex graph with vertices labeled $ 1,2,\dots,N $ is a cycle graph when there exists a permutation $ (v_1,v_2,\dots,v_N) $ of $ (1,2,\dots,N) $ such that: - For each $ i = 1,2,\dots,N-1 $ , there is an edge between vertices $ v_i $ and $ v_{i+1} $ . \- There is an edge between vertices $ v_N $ and $ v_1 $ . \- No other edges exist.

The input is given from Standard Input in the following format: > $ N $ $ M $ $ A_1 $ $ B_1 $ $ \vdots $ $ A_M $ $ B_M $

Output `Yes` if the given graph is a cycle graph; otherwise, print `No`.

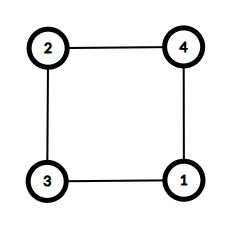
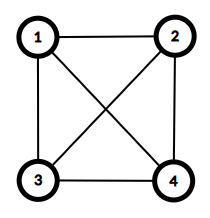
### Sample Explanation 1 The given graph is as follows, and this is a cycle graph.  ### Sample Explanation 2 The given graph is as follows, and this is not a cycle graph.  ### Constraints - $ 3 \le N \le 2\times 10^5 $ - $ 0 \le M \le 2\times 10^5 $ - $ 1 \le A_i, B_i \le N $ - The given graph is simple. - All input values are integers.