AT_abc404_c [ABC404C] Cycle Graph?

$ N $ 頂点 $ M $ 辺の単純無向グラフが与えられます。頂点には $ 1,2,\dots,N $ の番号が、辺には $ 1,2,\dots,M $ の番号がつけられており、辺 $ i $ は頂点 $ A_i $ と頂点 $ B_i $ を結んでいます。 このグラフがサイクルグラフであるか判定してください。 単純無向グラフとは単純無向グラフとは、自己ループや多重辺を含まず、辺に向きの無いグラフのことをいいます。 サイクルグラフとは頂点に $ 1, 2, \dots, N $ の番号が付けられた $ N $ 頂点のグラフがサイクルグラフであるとは、 $ (1, 2, \dots, N) $ を並べ変えて得られる数列 $ (v_1, v_2, \dots, v_N) $ であって、以下の条件を満たすものが存在することをいいます。 - $ i = 1, 2, \dots, N-1 $ に対して、頂点 $ v_i $ と $ v_{i+1} $ を結ぶ辺が存在する \- 頂点 $ v_N $ と $ v_1 $ を結ぶ辺が存在する \- それら以外の辺は存在しない

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ A_1 $ $ B_1 $ $ \vdots $ $ A_M $ $ B_M $

与えられたグラフがサイクルグラフであるなら `Yes`、そうでないなら `No` と出力せよ。

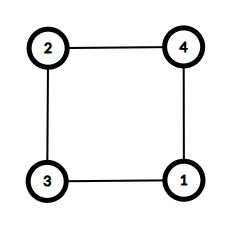
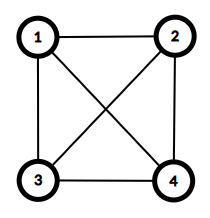
### Sample Explanation 1 与えられたグラフは以下の通りであり、これはサイクルグラフです。  ### Sample Explanation 2 与えられたグラフは以下の通りであり、これはサイクルグラフではありません。  ### Constraints - $ 3\leq N \leq 2\times 10^5 $ - $ 0 \leq M \leq 2\times 10^5 $ - $ 1 \leq A_i, B_i \leq N $ - 与えられるグラフは単純 - 入力は全て整数