AT_abc405_f [ABC405F] Chord Crossing

On a circle, $ 2N $ points are placed at equal intervals and numbered $ 1,2,\dots,2N $ in clockwise order starting from an arbitrary point. There are $ M $ line segments numbered $ 1,2,\dots,M $ connecting these points. Segment $ i $ connects points $ A_i $ and $ B_i $ . Here, $ A_i $ and $ B_i $ are distinct **even numbers**. It is guaranteed that no two of these segments share a point. Process $ Q $ queries. The $ j $ ‑th query is as follows: - You are given two distinct **odd numbers** $ C_j $ and $ D_j $ . Among the $ M $ segments $ 1,2,\dots,M $ , find how many share a point with the segment connecting points $ C_j $ and $ D_j $ .

The input is given from Standard Input in the following format: > $ N $ $ M $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_M $ $ B_M $ $ Q $ $ C_1 $ $ D_1 $ $ C_2 $ $ D_2 $ $ \vdots $ $ C_Q $ $ D_Q $

Output $ Q $ lines. The $ j $ -th line $ (1\leq j \leq Q) $ should contain the answer to the $ j $ ‑th query.

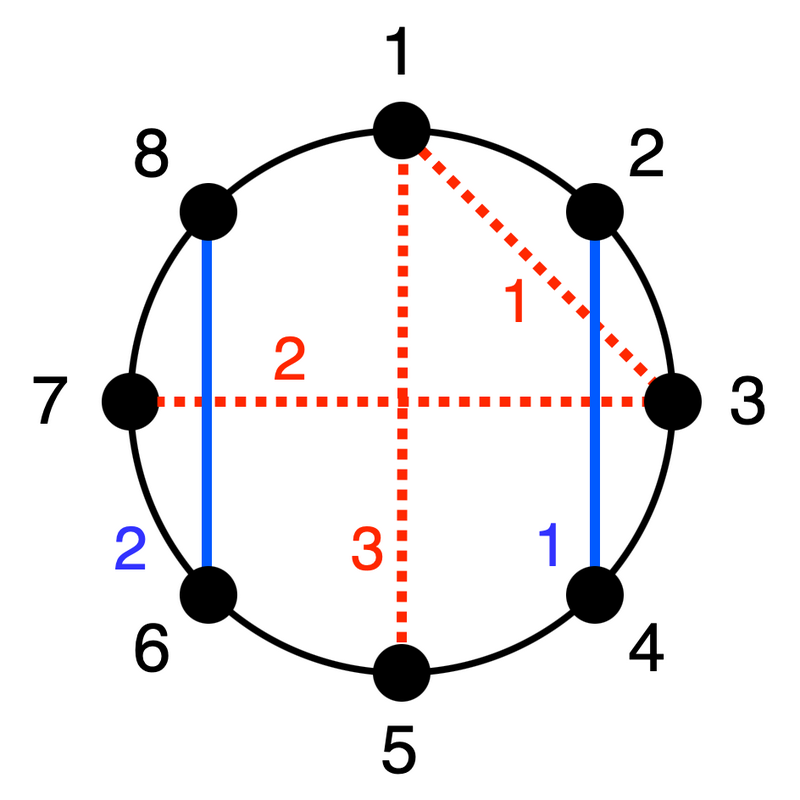
### Sample Explanation 1  The figure above illustrates Sample Input 1. Black dots are the $ 2N\ (=8) $ points, blue solid lines are the initial $ M\ (=2) $ segments, and red dashed lines are the $ Q\ (=3) $ query segments. - For the first query, the segment connecting points $ 1 $ and $ 3 $ intersects one initial segment: segment $ 1 $ . - For the second query, the segment connecting points $ 3 $ and $ 7 $ intersects two initial segments: segments $ 1 $ and $ 2 $ . - For the third query, the segment connecting points $ 1 $ and $ 5 $ intersects zero initial segments. ### Constraints - $ 2 \le N \le 10^6 $ - $ 1\leq M \leq \min\left(\lfloor\frac{N}{2}\rfloor, 2\times 10^5\right) $ - $ 1 \le Q \le 2 \times 10^5 $ - $ 1 \le A_i < B_i \le 2N $ - $ 1 \le C_j < D_j \le 2N $ - $ A_i $ and $ B_i $ are even. - $ C_j $ and $ D_j $ are odd. - For any $ i_1 $ and $ i_2 $ $ (i_1 \neq i_2) $ , segments $ i_1 $ and $ i_2 $ do not share a point. - All input values are integers.