AT_abc405_f [ABC405F] Chord Crossing

円周上に $ 2N $ 個の点が等間隔に並んでおり、ある点から始めて時計回りに $ 1,2,\dots,2N $ の番号が付けられています。 これらの点を結ぶ $ M $ 本の線分 $ 1,2,\dots,M $ が存在し、線分 $ i $ は点 $ A_i $ と点 $ B_i $ を結んでいます。 ここで、 $ A_i $ と $ B_i $ は相異なる **偶数** です。 また、これらの線分のうちのどの $ 2 $ つの線分も共有点を持たないことが保証されます。 $ Q $ 個のクエリを処理してください。 $ j $ 番目のクエリは以下の通りです。 - 相異なる $ 2 $ つの **奇数** $ C_j, D_j $ が与えられる。上で与えられた $ M $ 本の線分 $ 1,2,\dots,M $ のうち、点 $ C_j $ と点 $ D_j $ を結ぶ線分と共有点を持つものの本数を求めよ。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_M $ $ B_M $ $ Q $ $ C_1 $ $ D_1 $ $ C_2 $ $ D_2 $ $ \vdots $ $ C_Q $ $ D_Q $

$ Q $ 行出力せよ。 $ j\ (1\leq j \leq Q) $ 行目には、 $ j $ 番目のクエリに対する答えを出力せよ。

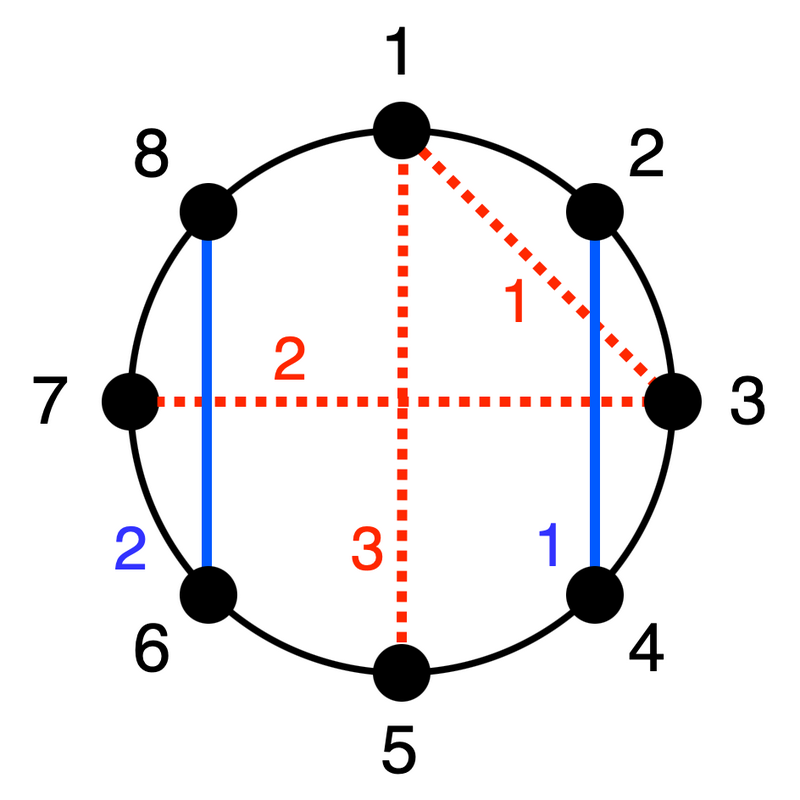
### Sample Explanation 1  上図は入力例 1 を図示したものであり、黒丸は $ 2N\ (=8) $ 個の点を、青い実線は最初に与えられる $ M\ (=2) $ 本の線分を、赤い点線はクエリで与えられる $ Q\ (=3) $ 本の線分をそれぞれ表しています。 - $ 1 $ 番目のクエリについて、最初に与えられた $ M $ 本の線分のうち、点 $ 1 $ と点 $ 3 $ を結ぶ線分と共有点を持つものは線分 $ 1 $ の $ 1 $ 本です。 - $ 2 $ 番目のクエリについて、最初に与えられた $ M $ 本の線分のうち、点 $ 3 $ と点 $ 7 $ を結ぶ線分と共有点を持つものは線分 $ 1,2 $ の $ 2 $ 本です。 - $ 3 $ 番目のクエリについて、最初に与えられた $ M $ 本の線分のうち、点 $ 1 $ と点 $ 5 $ を結ぶ線分と共有点を持つものは $ 0 $ 本です。 ### Constraints - $ 2\leq N \leq 10^6 $ - $ 1\leq M \leq \min\left(\lfloor\frac{N}{2}\rfloor, 2\times 10^5\right) $ - $ 1\leq Q \leq 2\times 10^5 $ - $ 1\leq A_i< B_i\leq 2N $ - $ 1\leq C_j< D_j\leq 2N $ - $ A_i, B_i $ は偶数 - $ C_j, D_j $ は奇数 - どの $ i_1, i_2\ (i_1 \neq i_2) $ についても、線分 $ i_1 $ と線分 $ i_2 $ は共有点を持たない - 入力は全て整数