AT_abc406_f [ABC406F] Compare Tree Weights

There is a tree $ T $ with $ N $ vertices. The vertices are labeled as vertex $ 1 $ , vertex $ 2 $ , $ \ldots $ , vertex $ N $ , and the edges are labeled as edge $ 1 $ , edge $ 2 $ , $ \ldots $ , edge $ (N-1) $ . Edge $ i $ $ (1\leq i\leq N-1) $ connects vertices $ U_i $ and $ V_i $ . Each vertex has a weight; initially, the weight of every vertex is $ 1 $ . You are given $ Q $ queries to process in order. Each query is of one of the following two types: - `1 x w` : Increase the weight of vertex $ x $ by $ w $ . - `2 y` : If edge $ y $ were removed, the tree $ T $ would be split into two subtrees (connected components). For each subtree, let its weight be the sum of the weights of its vertices. Output the difference between the weights of the two subtrees. For a query of the second type, it can be proved that removing any edge of $ T $ always splits it into exactly two subtrees. Note that queries of the second type do not actually delete remove the edge.

The input is given from Standard Input in the following format: > $ N $ $ U_1 $ $ V_1 $ $ U_2 $ $ V_2 $ $ \vdots $ $ U_{N-1} $ $ V_{N-1} $ $ Q $ $ \mathrm{query}_1 $ $ \mathrm{query}_2 $ $ \vdots $ $ \mathrm{query}_Q $ Each query $ \mathrm{query}_i $ $ (1\leq i\leq Q) $ is given in one of the following formats: ``` 1 x w ``` ``` 2 y ```

Let $ K $ be the number of queries of the second type. Output $ K $ lines; the $ i $ -th line ( $ 1 \leq i \leq K $ ) should contain the answer to the $ i $ -th query of the second type.

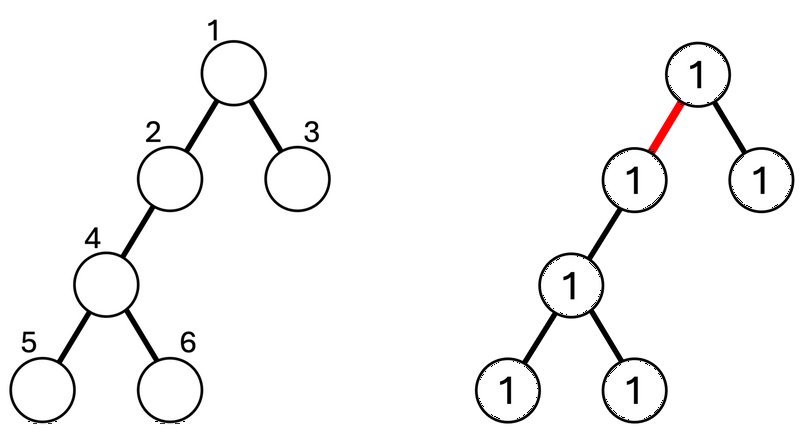
### Sample Explanation 1 The structure of the tree $ T $ and the vertex numbering are as shown on the left of the figure below. Initially, the weight of every vertex is $ 1 $ . In the 1st query, consider deleting edge $ 1 $ . The tree splits into the subtree containing vertex $ 1 $ and the subtree containing vertex $ 2 $ . The subtree with vertex $ 1 $ has weight $ 2 $ ; the subtree with vertex $ 2 $ has weight $ 4 $ . Output the difference, $ 2 $ (figure below, right).  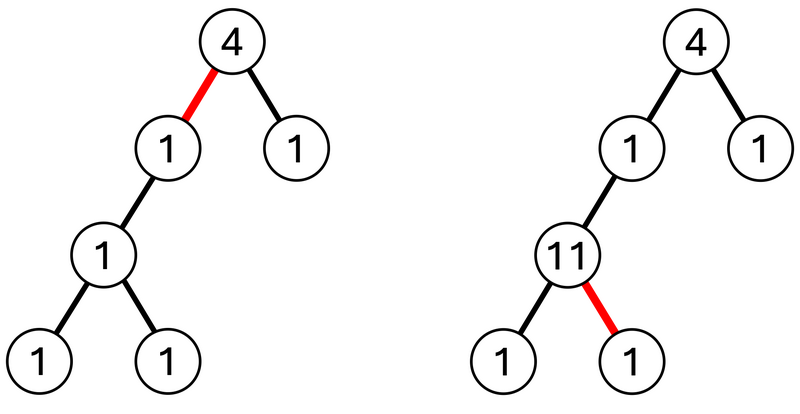The 2nd query increases the weight of vertex $ 1 $ by $ 3 $ . In the 3rd query, consider deleting edge $ 1 $ . The subtree with vertex $ 1 $ has weight $ 5 $ ; the subtree with vertex $ 2 $ has weight $ 4 $ . Output the difference, $ 1 $ (figure below, left). The 4th query increases the weight of vertex $ 4 $ by $ 10 $ . In the 5th query, consider deleting edge $ 5 $ . The tree splits into the subtree containing vertex $ 4 $ and the subtree consisting only of vertex $ 6 $ . The subtree with vertex $ 4 $ has weight $ 18 $ ; the subtree with vertex $ 6 $ has weight $ 1 $ . Output the difference, $ 17 $ (figure below, right).  Thus, output the answers to the queries of second type in order: $ 2 $ , $ 1 $ , and $ 17 $ , separated by newlines. ### Constraints - $ 2 \leq N \leq 3 \times 10^5 $ - $ 1 \leq U_i, V_i \leq N $ - $ 1 \leq Q \leq 3 \times 10^5 $ - $ 1 \leq x \leq N $ - $ 1 \leq w \leq 1000 $ - $ 1 \leq y \leq N-1 $ - All input values are integers. - The given graph is a tree. - There is at least one query of the second type.